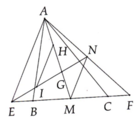
Cho tam giác ABC đường trung tuyến AM và trọng tâm G. Trên tia đối của tia MA lấy các điểm I và K sao cho MI = MG, IK = IG. Gọi N là trung điểm của CK. Chứng minh rằng ba điểm B, I, N thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2016
Tam giác ABC có: G là giao điểm của trung tuyến AM và BN (gt)
=> G là trọng tâm tam giác ABC
=>GM = 1/2 GA (đ/lí 3 trung tuyến của tam giác) (1)
Có GM = MK (gt)
Mà GM + MK = GK
=> GM = MK = 1/2 GK (2)
Từ (1)(2) => GA = GK
b, Xét tam giác BMK và tam giác CMG
BM = CM (gt)
góc BMK = góc CMG (đối đỉnh)
MK = MG (gt)
=> tam giác BMK = tam giác CMG (c.g.c)
c, Xét tam giác ABM và tam giác QCM
MA = QM (gt)
góc AMB = góc QMC ( đối đỉnh)
MB = MC (gt)
=> tam giác ABM = tam giác QCM(c.g.c)
=> góc BAQ = góc CQA ( cặp góc tương ứng)
=> AB // QC ( vì góc BAQ và góc CQA là 2 góc so le trong (3)
Xét tam giác BAN và tam giác ICN
BN = NI (gt)
góc BNA = góc INC (đối đỉnh)
AN = CN (gt)
=> tam giác BAN = tam giác ICN (c.g.c)
=> góc BAN = góc ICN (cặp góc tương ứng)
=> AB // CI (vì góc BAN và góc ICN là 2 góc so le trong) (4)
Từ (3)(4) => Q, C, I thẳng hàng
28 tháng 4 2023
a: Xet ΔBMG và ΔCME có
MB=MC
góc BMG=góc CME
MG=ME
=>ΔBMG=ΔCME
b: Xet tứ giác BGCE co
M là trung điểm chung của BC và GE
=>BGCE là hình bình hành
=>BG//CE
c: Xét ΔABE co
AI,BG là trung tuyến
AI cắt BG tại F
=>F là trọng tâm
=>E,F,N thẳng hàng