Một hình tròn được chia thành 10 ô quạt , mỗi ô người ta đặt 1 viên bi.Nếu ta cứ di chuyển các viên bi theo quy luật :mỗi lần lấy ở hai ô bất kì một viên bi , chuyển sang ô liền kề theo chiều ngược nhau thì có thể chuyển tất cả các viên bi về 1 ô được không?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
28 tháng 6 2023
-
Để chứng minh sau hữu hạn bước sẽ không thực hiện chuyển bi được nữa, ta quan sát rằng mỗi bước chuyển bi, tổng số bi trong các ô liên tiếp tăng lên 1 đơn vị. Ban đầu có 2023 viên bi, và sau mỗi bước chuyển bi, tổng số bi trong các ô liên tiếp tăng lên 1 đơn vị. Vì số lượng ô là vô hạn, nên sau một số bước chuyển bi, tổng số bi trong các ô liên tiếp sẽ vượt quá 2023. Do đó, sau hữu hạn bước sẽ không thực hiện chuyển bi được nữa.
-
Để chứng minh P, Q, D, H đồng viên, ta sử dụng tính chất của tam giác nội tiếp và ngoại tiếp.
Vì tam giác ABC nội tiếp (O), ngoại tiếp (I), nên ta có:
- Giao điểm của EF và BC là D.
- Giao điểm của AG và EF là H.
- Giao điểm của AG và (I) là M.
Ta cần chứng minh P, Q, D, H đồng viên, tức là chúng nằm trên một đường thẳng.
Áp dụng định lí Pascal cho đường tròn ngoại tiếp (O) và đường tròn nội tiếp (I), ta có:
- Điểm P = AB ∩ EF.
- Điểm Q = AC ∩ EF.
- Điểm D = BC ∩ PQ.
Vì P, Q, D nằm trên cùng một đường thẳng PQ, nên ta chỉ cần chứng minh H nằm trên đường thẳng PQ.
Áp dụng định lí Pascal cho đường tròn ngoại tiếp (O) và đường tròn nội tiếp (I), ta có:
- Điểm H = AG ∩ EF.
- Điểm M = BC ∩ OI.
- Điểm D = PQ ∩ OI.
Vì H, M, D nằm trên cùng một đường thẳng OI, nên H nằm trên đường thẳng PQ.
Vậy ta đã chứng minh được rằng P, Q, D, H đồng viên.
DS
31 tháng 7 2019
cách làm chi tiết bài số 7 nhá.ta dự đoán(theo kinh nghiệm khi giải mấy bài cơ bản kiểu này) là khi người 2 bốc bao nhiêu thì người 1 bốc x- số người 2 vừa bốc.làm thế thì CHO DÙ NGƯỜI 2 BỐC BAO NHIÊU THÌ TỔNG 1 LƯỢT VẪN LÀ X.vì vậy chúng ta sẽ đưa người 2 vào vòng lặp này bằng lần bốc đầu và chiến thắng bằng lần x cuối cùng.vì bốc từ 11-20 nên ta phải chọn x(ta có thể chọn x) sao cho người 2 bốc bao nhiêu ta vx bốc đc x- số đó.vì vậy x phải là 11+20=31.vì vậy lượt đầu ta bốc 5 viên.còn lại ng 2 bốc bao nhiêu thì ta bốc 31- bấy nhiêu thì ta thắng vì 2015 chia hết cho 31
DS
31 tháng 7 2019
bài số 8 nhé.ko thể.bàn cờ mất 2 ô ở 2 góc chéo nên ko mất tính tổng quát giả sử mất 2 ô màu trắng.nhận xét cho dù có xếp 1x2 như thế nào thì cx che hết 1 ô đen và 1 ô trắng.vì vậy để che hết bàn cờ chứng tỏ nếu che 32 ô đen(toàn bộ ô đen trên bàn cờ) thì cx PHẢI che mất 32 ô trắng.nhưng thực tế có 30 ô trắng vì vậy ko thể.
hình như 1 số bài thiếu thông tin???
CM
27 tháng 5 2018
Số viên bi còn lại trên bàn cờ là 150 - 21 = 129
Vì 139 = 64×2 + 1 nên theo nguyên lý Dirichle sẽ tồn tại ít nhất 3 viên bi nằm trong cùng 1 ô, và 3 viên này khoảng cách giữa 2 viên tùy ý sẽ nhỏ hơn đường chéo ô vuông = 2cm
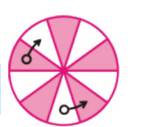
Trước tiên ta tô màu xem kẽ các ô hình quạt , như vậy sẽ có 5 ô được tô màuvà 5 ô ko đc tô màu
Ta có nhận xét : Nếu di chuyển 1 bi ở bi màu và 1 bi ở ô trắng thì tổng số bi ở 5 ô màu không đổi . Nếu di chuyển ở 2 ô màu mỗi ô 1 bi thì tổng số bi ở 5 ô màu giảm đi 2 . Nếu di chuyển ở 2 ô trắng mỗi ô một bi thì tổng số ở 5 ô màu tăng lên 2 .
Vậy tổng số bi ở 5 ô màu hoặc không đổi hoặc giảm đi 2 hoặc tăng lên 2 .Nói khác tổng số bi ở 5 ô màu sẽ ko thay đổi tính chẵn lẻ so với ban đầu . Ban đầu tổng số bi ở 5 ô màu là 5 viên nên sau hữu hạn dần di chuyển bi theo quy luật trên thì tổng số bi ở 5 ô màu luôn khác 0 và khác 10 .do đó ko thể chuyển tất cả các viên bi về cùng 1 ô