cho hàm số y=3x . tìm M(x;y) thuộc đồ thị hàm số biết 17x+4y =58
bạn ywww giúp hoàng vs # bão đe #
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 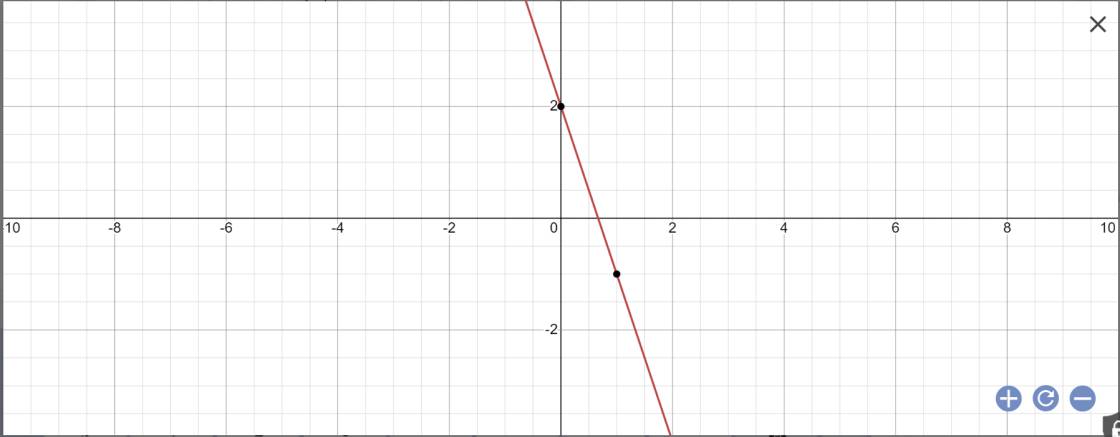
b: Để đồ thị hàm số y=(m+1)x-3 song song với đồ thị hàm số y=-3x+2 thì \(\left\{{}\begin{matrix}m+1=-3\\2\ne-3\left(đúng\right)\end{matrix}\right.\)
=>m+1=-3
=>m=-4

Để hàm số y=(2m-3)x-5m+1 là hàm số bậc nhất thì \(2m-3\ne0\)
\(\Leftrightarrow2m\ne3\)
\(\Leftrightarrow m\ne\dfrac{3}{2}\)
a) Để hàm số y=(2m-3)x-5m+1 đồng biến trên R thì \(2m-3>0\)
\(\Leftrightarrow2m>3\)
hay \(m>\dfrac{3}{2}\)
Vậy: Khi hàm số y=(2m-3)x-5m+1 đồng biến trên R thì \(m>\dfrac{3}{2}\)
b) Để đồ thị hàm số y=(2m-3)x-5m+1 song song với đường thẳng y=3x+5 thì \(\left\{{}\begin{matrix}2m-3=3\\-5m+1\ne5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m=6\\-5m\ne4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne\dfrac{-4}{5}\end{matrix}\right.\Leftrightarrow m=3\left(nhận\right)\)
Vậy: Để đồ thị hàm số y=(2m-3)x-5m+1 song song với đường thẳng y=3x+5 thì m=3
a. Tìm m để hàm số đồng biến.
Để hàm số trên đồng biến. => 2m-3 > 0
<=> 2m > 3
<=> m > 3/2
b. Tìm m để đồ thị hàm số (1) song song đường thẳng y=3x-5
Để đồ thị hàm số (1) song song đường thẳng y = 3x - 5
=> 2m-3 = 3 và -5m+1 khác - 5
<=> m = 3 và m khác 6/5
<=> m = 3 (tm)
c. Tính góc tạo bởi đường thẳng y=3x-5 với trục Ox
Gọi góc tạo bởi đường thẳng y=3x-5 với trục Ox là a (a>0)
=> tan a = |3|
=> tan a = 3
=> góc a = 71o 33'

Để hàm số y lẻ thì f(-x) = -f(x), nghĩa là:
-x3 - 3x + m = -x3 - 3x -m
Do đó m = -m ↔ m = 0.
Mình nghĩ vậy thôi không biết đúng không.

\(f\left(-x\right)=\left(-x\right)^3+3\cdot\left(-x\right)+m\)
\(=-x^3-3x+m\)
Để hàm số lẻ thì f(-x)=-f(x)
=>m=-m
=>2m=0
hay m=0

a/ Hàm hằng có dạng y = k với k là một hằng số
Vậy (2-3m).x = 0 => m = 2/3 => Hàm hằng là y = m-2
b/
Phương trình hoành độ giao điểm : (2-3m)x+m-2 = 3x+2
Vì đths đã cho cắt đường thẳng y = 3x+2 tại điểm trên trục tung nên x = 0
Suy ra m-2 = 2 => m = 4

\(y'=3x^2-6x+m\)
Hàm nghịch biến trên khoảng đã cho khi và chỉ khi \(y'\le0\) ; \(\forall x\in\left(-1;0\right)\)
\(\Leftrightarrow m\le-3x^2+6x\) ; \(\forall x\in\left(-1;0\right)\)
\(\Leftrightarrow m\le\min\limits_{\left(-1;0\right)}\left(-3x^2+6x\right)\)
Xét hàm \(f\left(x\right)=-3x^2+6x\) trên \(\left(-1;0\right)\)
\(-\dfrac{b}{2a}=1\notin\left(-1;0\right)\) ; \(f\left(-1\right)=-9\) ; \(f\left(0\right)=0\)
\(\Rightarrow m\le-9\)

giao diem co hoanh do la 3x-1=x+3=>x=2
toa do giao diem la A(2,5)
5=(m-2).2+m+2
5=2m-4+m+2=3m-2
3m=7
m=7/3

a, để hàm số đồng biến thì\(m-1>0\Rightarrow m>1\)
b, khi m=3 thì \(y=\left(3-1\right)x+2.3+1\Rightarrow y=2x+7\)
bạn tự vẽ đồ thị hàm số trên nhé do trên này khó vẽ
c, để đồ thị hàm số (1) song song vs S
dt' y= 3x+1 thì \(\left\{{}\begin{matrix}m-1=3\\2m+1\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=4\\m\ne1\end{matrix}\right.\Leftrightarrow m=4\)
e, không rõ đề