Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Để (d)//y=-3x+2 thì m-1=-3
=>m=-2
c:
PTHĐGĐ là:
(m-1)x-4=x-7
=>(m-2)x=-3
Để hai đường cắt nhau tại một điểm nằm bên trái trục tung thì m-1<>1 và -3/(m-2)<0
=>m<>2 và m-2>0
=>m>2

Hàm số y = (m+1)x -2m là hàm bậc nhất khi m+1 ≠ 0 ⇔ m ≠ - 1
a) Hàm số nghịch biến trên R khi a < 0 ⇔ m + 1< 0 ⇔ m < - 1
kết hợp với điều kiện. Vậy m < -1
b) Khi m = 1 ta được: y = (1+1)x - 2.1 hay y = 2x - 2
Đồ thị hàm số y = 2x - 2 đi qua hai điểm A(0;-2) và B(1;0)
c) Đồ thị của hai hàm số song song với nhau khi \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+1=3\\-2m\ne6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2\\m\ne-3\end{matrix}\right.\)
kết hợp với điều kiện. Vậy m = 2
Tham Khảo:
Hàm số y = (m+1)x -2m là hàm bậc nhất khi m+1 ≠ 0 ⇔ m ≠ - 1
a) Hàm số nghịch biến trên R khi a < 0 ⇔ m + 1< 0 ⇔ m < - 1
kết hợp với điều kiện. Vậy m < -1
b) Khi m = 1 ta được: y = (1+1)x - 2.1 hay y = 2x - 2
Đồ thị hàm số y = 2x - 2 đi qua hai điểm A(0;-2) và B(1;0)
c) Đồ thị của hai hàm số song song với nhau khi
kết hợp với điều kiện. Vậy m = 2

a) Khi m =2 thì y = 3x - 1
(Bạn tự vẽ tiếp)
b) Để \((d)//(d_{1})\) thì \(\begin{cases} 2m-1=-3\\ -3m+5\neq2 \end{cases} \) ⇔ \(\begin{cases} m=-1\\ m\neq1 \end{cases} \) ⇔ \(m=-1\)
c)
Để \((d) ⋂ (d1)\) thì \(2m-1\neq-3 \) ⇔ \(m\neq-1\)
Giao điểm của 2 đường thẳng thuộc trục tung => x=0
Khi đó, ta có: \(y=-3.0+2=2\)
⇒ Điểm \((0;2)\) cũng thuộc đường thẳng (d)
⇒ \(2=(2m-1).0-3m+5\) ⇔ \(m=1\) (TM)

a> gọi y=(m-2)x+n là (d)
để (d) là hsbn thì m khác 2, với mọi n thuộc R
b> hàm số đồng biến khi m>2
nghịch biến khi m<2
c> điều kiện để (d) // (d'): y=2x-1 <=> m-2=2 <=>m=4
và n khác -1
vậy để (d) // (d') <=> m=4, m khác 2, n khác -1
d> điều kiện để (d) cắt (d''): y=-3x+2 <=> m-2=-3 <=> m khác -1
vậy để (d) cắt (d'') <=> m khác 2, m khác -1
e> để (d) trùng (d'''): y=3x-2 <=> m-2=3 <=> m=5
và n = -2
vậy để d//d''' <=> m khác 2, m=5, n=-2
f> vì d đi qua A(1;2) => 2=m-2+n <=> m+n=4 (1). vì d đi qua B(3;4) => 4=3m-6+n <=> 3m+n = 10 (2)
lấy (2) trừ (1) <=> 2m=6 <=> m= 3 => n=1

1. Đồ thị của hàm số đi qua điểm \(M\left(2;3\right)\) nên giá trị hoành độ và tung độ của \(M\) là nghiệm của phương trình đường thẳng trên, tức:
\(3=m\cdot2+m-6\Leftrightarrow m=3\left(TM\right)\)
2. Đồ thị hàm số song song với đường thẳng \(\left(d\right):y=3x+2\), khi: \(\left\{{}\begin{matrix}m=3\\m-6\ne2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne8\end{matrix}\right.\Rightarrow m=3\left(TM\right)\)
3. Gọi \(P\left(x_0;y_0\right)\) là điểm cố định mà đồ thị hàm số đi qua với mọi giá trị \(m\).
Khi đó: \(mx_0+m-6=y_0\Leftrightarrow\left(x_0+1\right)m-\left(y_0+6\right)=0\left(I\right)\)
Suy ra, phương trình \(\left(I\right)\) có vô số nghiệm, điều này xảy ra khi: \(\left\{{}\begin{matrix}x_0+1=0\\y_0+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=-6\end{matrix}\right.\).
Vậy: Điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị \(m\) là \(P\left(-1;-6\right)\).

c: Thay x=1 và y=-4 vào (d), ta được:
\(m-1+m+3=-4\)
\(\Leftrightarrow2m=-6\)
hay m=-3
a: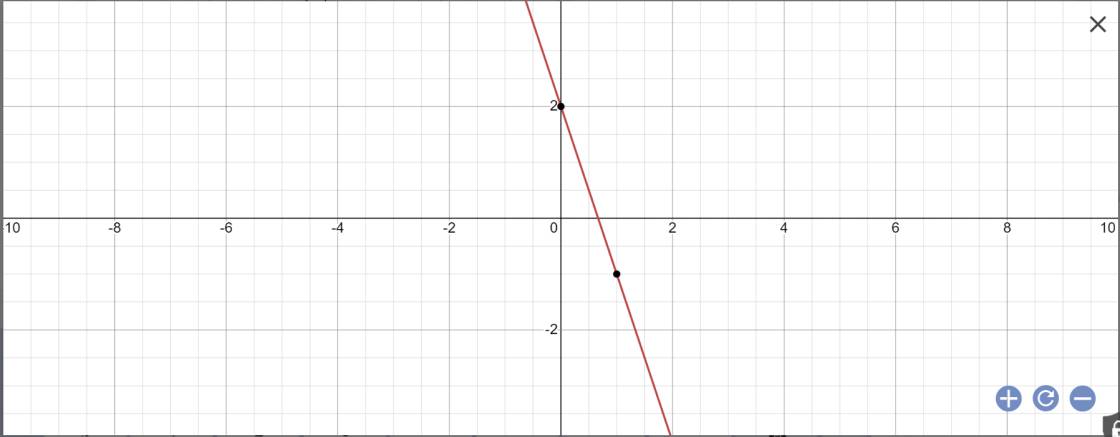
b: Để đồ thị hàm số y=(m+1)x-3 song song với đồ thị hàm số y=-3x+2 thì \(\left\{{}\begin{matrix}m+1=-3\\2\ne-3\left(đúng\right)\end{matrix}\right.\)
=>m+1=-3
=>m=-4