Cho đường tròn tam O bán kính R .đường kính AB .kẻ tiếp tuyến Ax lấy tiếp tuyến đó 1 điểm P sao cho AP>R .từ P kẻ tiếp tuyến tiếp xúc với (O)
a.CM:tứ giác APMO nội tiếp đường tròn
b.chứng minh BM//OP
c.đường thẳng vuông góc AB ở O cắt tia BM tại N .Chứng minh tứ giác OBNP là hình bình hành
d.biết AN cắt OP tại K .PM cắt ON tại I .PN và OM kéo dài cắt nhau tại J .chứng minh I,J,K thẳng hàng




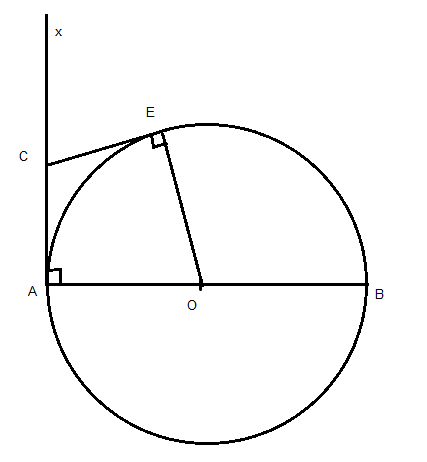
a, PM là tiếp tuyến
=> PM vuông góc vớiOM
=>OMP=90
PA là tiếp tuyến
=>PA vuông AO
=>PAO=90
=>OMP+ PAO=180
=>Tứ giác APMO nội tiếp đường tròn
b, Góc AMB là góc nội tiếp hẳn nửa đường tròn
=> AMB=90=>AM vuông góc với MB
Lại có PA và PM là 2 tiếp tuyến cắt nhau tại M => PA=PM
=> P thuộc đường trung trực của AM
mà OA=OM
=> O thuộc đường trung trực của AM
=> PO là đường trung trực của AM => PO vuông góc với AM
=> PO // MB ( vì cùng vuông góc với AM)