Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

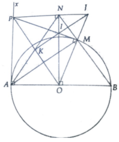
a, HS tự làm
b, Ta có OP ⊥ AM, BM ⊥ AM => BM//OP
c, chứng minh ∆AOP = ∆OBN => OP=BN
lại có BN//OP do đó OPNB là hình bình hành
d, Ta có ON ⊥ PI, PM ⊥ JO mà PM ∩ ON = I => I là trực tâm ∆POJ => JI ⊥ PO(1)
Chứng minh PAON hình chữ nhật => K trung điểm PO
Lại có A P O ^ = O P I ^ = I O P ^ => ∆IPO cân tại I => IKPO (2)
Từ (1),(2) => J,I,K thẳng hàng

c) Tứ giác OAPN có PA//ON (cùng vuông góc OA) ; OA//PN nên là hình bình hành mà có góc A vuông do đó là hình chữ nhật
Tứ giác POMN có MN//PO nên là hình thang (1)
Mặt khác PA = ON (OAPN là hcn) ; PA = PM(2 tiếp tuyến cắt nhau) => ON = PM (2)
Từ (1) và (2) => POMN là hính thang cân => góc POM = góc OPN hay góc POJ = góc OPJ. Vậy tam giác OPJ cân đỉnh J
mà K là trung điểm OP(OAPN là hcn) => JK là đường trung tuyến, đường cao => JK vuông góc OP (3)
Trong tam giác JOP có ON vuông góc PJ ; PM vuông góc OJ nên I là trực tâm tg OPJ => JI vuông góc OP (4)
Từ (3) và (4) => J, I, K thẳng hàng

a, Xét tứ giác APMO có
^PAO + ^PMO = \(90^0\)+\(90^0\)=1800
mà ^PAO và ^PMO là 2 góc đối nhau
=> tứ giác APMO nội tiếp (đccm)
b, Có PA=PM (t/c 2 tiếp tuyến cắt nhau)
OA=OM (bán kính (O))
=> PO là đ.t.trực của AM => PO⊥AM (1)
Có ^AMB là góc nt chắn nửa (O) => ^AMB = \(90^0\) hay AM⊥MB (2)
Từ (1),(2) => PO//BM
c, Xét ΔPAO và ΔNOB có
^PAO= ^NOB=\(90^0\) (Ax là tt, ON⊥AB)
^POA= ^NBO ( PO//BM)
OA =OB
=> ΔPAO= ΔNOB (gcg)
=>PO=BN
mà PO//BN ( câu b)
=>POBN là hbh
d, Có POBN là hbh =>PN//OB
mà ON⊥OB
=> ON⊥PN (từ ⊥ đến //)
Xét ΔPJO có PM⊥OJ (PM là tt)
ON⊥CJ (cmt)
PM\(\cap\)ON =\(\left\{I\right\}\)
=> I là trực tâm △PJO
=>JI⊥PO
các bạn c/m IK⊥PO là ra nhé
có cái mị k ngoặc đc ( *thông cảm a*)