Xác định hệ số a, b, c biết rằng;
\(2x^2-3x-4=ax^2+bx-\left(c+1\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Bậc là 2
Hệ số cao nhất là -7
Hệ số tự do là 1
b: Thay x=2 vào A=0, ta được:
\(a\cdot2^2-3\cdot2-18=0\)
\(\Leftrightarrow4a=24\)
hay a=6
c: Ta có: C+B=A
nên C=A-B
\(=6x^2-3x-18-1-4x+7x^2\)
\(=13x^2-7x-19\)

Ta có T = ( a x + 4 ) ( x 2 + b x – 1 )
= a x . x 2 + a x . b x + a x . ( - 1 ) + 4 . x 2 + 4 . b x + 4 . ( - 1 ) = a x 3 + a b x 2 – a x + 4 x 2 + 4 b x – 4 = a x 3 + ( a b x 2 + 4 x 2 ) + ( 4 b x – a x ) – 4 = a x 3 + ( a b + 4 ) x 2 + ( 4 b – a ) x – 4
Theo bài ra ta có
( a x + 4 ) ( x 2 + b x – 1 ) = 9 x 3 + 58 x 2 + 15 x + c đúng với mọi x
ó a x 3 + ( a b + 4 ) x 2 + ( 4 b – a ) x – 4 = 9 x 3 + 58 x 2 + 15 x + c đúng với mọi x.
ó a = 9 a b + 4 = 58 4 b - a = 15 - 4 = c ó a = 9 9 . b = 54 4 b - a = 15 c = - 4 ó a = 9 b = 6 c = - 4
Vậy a = 9, b = 6, c = -4
Đáp án cần chọn là: B

Đáp án B
Do hệ phương trình đã cho có nghiệm là (1; 1) nên:
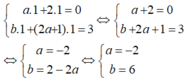
Vậy a = -2; b = 6

\(C\left(x\right)=ax+b\)
\(\Rightarrow\hept{\begin{cases}C\left(2\right)=2a+b\\C\left(1\right)=a+b\end{cases}}\)
hay \(\hept{\begin{cases}2a+b=-1\left(1\right)\\a+b=0\left(2\right)\end{cases}}\)
Lấy (1) - (2), ta được: \(a=-1\)
\(\Rightarrow b=1\)
Vậy a = -1; b = 1

a) Vì đồ thị hàm số y=ax+3 đi qua điểm A(-1;1) nên Thay x=-1 và y=1 vào hàm số y=ax+3, ta được:
\(-1\cdot a+3=1\)
\(\Leftrightarrow-a+3=1\)
\(\Leftrightarrow-a=-2\)
hay a=2
Vậy: Hệ số a=2
Đồng nhất hệ số theo quy tắc: "Hai đa thức bằng nhau khi các hệ số ở đồng bậc bằng nhau." là ra ấy mà=)
Thôi làm luôn:
Do \(2x^2-3x-4=ax^2+bc-\left(c+1\right)\) .Đồng nhất hệ số hai vế ta được:
\(\hept{\begin{cases}a=2\\b=-3\\c+1=4\end{cases}}\Leftrightarrow\hept{\begin{cases}a=2\\b=-3\\c=3\end{cases}}\)