7x (16x2-1)=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(3x^2+4x=2x\Leftrightarrow3x^2+2x=0\Leftrightarrow x\left(3x+2\right)=0\Leftrightarrow x=-\dfrac{2}{3};x=0\)
b, \(25x^2-\dfrac{64}{100}=0\Leftrightarrow25x^2-\left(\dfrac{8}{10}\right)^2=0\Leftrightarrow\left(5x-\dfrac{8}{10}\right)\left(5x+\dfrac{8}{10}\right)=0\)
\(\Leftrightarrow x=\dfrac{4}{25};x=-\dfrac{4}{25}\)
c, \(x^4-16x^2=0\Leftrightarrow x^2\left(x-4\right)\left(x+4\right)=0\Leftrightarrow x=0;x=-4;x=4\)
sửa d, \(x^2+x=6\Leftrightarrow x^2+x-6=0\Leftrightarrow\left(x-2\right)\left(x+3\right)=0\Leftrightarrow x=-3;x=2\)
e, \(x^2-7x=-12\Leftrightarrow x^2-7x+12=0\Leftrightarrow\left(x-4\right)\left(x-3\right)=0\Leftrightarrow x=3;x=4\)
e: ta có: \(x^2-7x=-12\)
\(\Leftrightarrow x^2-7x+12=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)

`4-x=2(x-4)^2`
`<=>4-x=2(x^2-8x+16)`
`<=> 4-x=2x^2 - 16x+32`
`<=> 4-x-2x^2+16x-32=0`
`<=> -2x^2 +15x-28=0`
`<=> -(2x^2-15x+28)=0`
`<=>-(2x^2-7x-8x+28)=0`
`<=> - [x(2x-7) - 4(2x-7)]=0`
`<=> -(2x-7)(x-4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}-2x+7=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}-2x=-7\\x=4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=4\end{matrix}\right.\)
__
`(x^2 +1) (x-2)+2x=4`
`<=> x^3 -2x^2 +x-2+2x-4=0`
`<=> x^3 -2x^2 +3x-6=0`
`<=> (x^3+3x)-(2x^2+6)=0`
`<=> x(x^2 +3) -2(x^2+3)=0`
`<=>(x^2+3)(x-2)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x^2+3=0\\x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x\in\varnothing\\x=2\end{matrix}\right.\)
__
`x^4 -16x^2=0`
`<=> x^2 (x^2 -16)=0`
`<=>x^2(x-4)(x+4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x^2=0\\x-4=0\\x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
\(4-x=2\left(x-4\right)^2\)
\(\Leftrightarrow4-x=2\left(x^2-8x+16\right)\)
\(\Leftrightarrow4-x=2x^2-16x+32\)
\(\Leftrightarrow2x^2-15x+28=0\)
\(\Leftrightarrow2x^2-7x-8x+28=0\)
\(\Leftrightarrow x\left(2x-7\right)-4\left(2x-7\right)=0\)
\(\Leftrightarrow\left(2x-7\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-7\\x=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=4\end{matrix}\right.\)
___________
\(\left(x^2+1\right)\left(x-2\right)+2x=4\)
\(\Leftrightarrow x^3-2x^2+x-2+2x=4\)
\(\Leftrightarrow x^3-2x^2+3x-2-4=0\)
\(\Leftrightarrow x^3-2x^2+3x-6=0\)
\(\Leftrightarrow x^2\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x^2+3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=-3\left(\text{vô lý}\right)\\x=2\left(tm\right)\end{matrix}\right.\)
\(\Leftrightarrow x=2\)
________________
\(x^4-16x^2=0\)
\(\Leftrightarrow\left(x^2\right)^2-\left(4x\right)^2=0\)
\(\Leftrightarrow\left(x^2-4x\right)\left(x^2+4x\right)=0\)
\(\Leftrightarrow x\left(x-4\right)x\left(x+4\right)=0\)
\(\Leftrightarrow x^2\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=0\\x-4=0\\x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)

`a)16x^2-24x+9=25`
`<=>(4x-3)^2=25`
`+)4x-3=5`
`<=>4x=8<=>x=2`
`+)4x-3=-5`
`<=>4x=-2`
`<=>x=-1/2`
`b)x^2+10x+9=0`
`<=>x^2+x+9x+9=0`
`<=>x(x+1)+9(x+1)=0`
`<=>(x+1)(x+9)=0`
`<=>` \(\left[ \begin{array}{l}x=-9\\x=-1\end{array} \right.\)
`c)x^2-4x-12=0`
`<=>x^2+2x-6x-12=0`
`<=>x(x+2)-6(x+2)=0`
`<=>(x+2)(x-6)=0`
`<=>` \(\left[ \begin{array}{l}x=-2\\x=6\end{array} \right.\)
`d)x^2-5x-6=0`
`<=>x^2+x-6x-6=0`
`<=>x(x+1)-6(x+1)=0`
`<=>(x+1)(x-6)=0`
`<=>` \(\left[ \begin{array}{l}x=6\\x=-1\end{array} \right.\)
`e)4x^2-3x-1=0`
`<=>4x^2-4x+x-1=0`
`<=>4x(x-1)+(x-1)=0`
`<=>` \(\left[ \begin{array}{l}x=1\\x=-\dfrac14\end{array} \right.\)
`f)x^4+4x^2-5=0`
`<=>x^4-x^2+5x^2-5=0`
`<=>x^2(x^2-1)+5(x^2-1)=0`
`<=>(x^2-1)(x^2+5)=0`
Vì `x^2+5>=5>0`
`=>x^2-1=0<=>x^2=1`
`<=>` \(\left[ \begin{array}{l}x=1\\x=-1\end{array} \right.\)

\(a,\Leftrightarrow x^2\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\\ b,\Leftrightarrow\left(3x-5\right)^2=0\Leftrightarrow x=\dfrac{5}{3}\)

a, \(x^4-4x^3-6x^2-4x+1=0\)(*)
<=> \(x^4+4x^2+1-4x^3-4x+2x^2-12x^2=0\)
<=> \(\left(x^2-2x+1\right)^2=12x^2\)
<=>\(\left(x-1\right)^4=12x^2\) <=> \(\left[{}\begin{matrix}\left(x-1\right)^2=\sqrt{12}x\\\left(x-1\right)^2=-\sqrt{12}x\end{matrix}\right.\)<=> \(\left[{}\begin{matrix}x^2-2x+1-\sqrt{12}x=0\left(1\right)\\x^2-2x+1+\sqrt{12}x=0\left(2\right)\end{matrix}\right.\)
Giải (1) có: \(x^2-2x+1-\sqrt{12}x=0\)
<=> \(x^2-2x\left(1+\sqrt{3}\right)+\left(1+\sqrt{3}\right)^2-\left(1+\sqrt{3}\right)^2+1=0\)
<=> \(\left(x-1-\sqrt{3}\right)^2-3-2\sqrt{3}=0\)
<=> \(\left(x-1-\sqrt{3}\right)^2=3+2\sqrt{3}\) <=> \(\left[{}\begin{matrix}x-1-\sqrt{3}=\sqrt{3+2\sqrt{3}}\\x-1-\sqrt{3}=-\sqrt{3+2\sqrt{3}}\end{matrix}\right.\) <=> \(\left[{}\begin{matrix}x=\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\left(ktm\right)\\x=-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\left(tm\right)\end{matrix}\right.\)
=> \(x=-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\)
Giải (2) có: \(x^2-2x+1+\sqrt{12}x=0\)
<=> \(x^2-2x\left(1-\sqrt{3}\right)+\left(1-\sqrt{3}\right)^2-\left(1-\sqrt{3}\right)^2+1=0\)
<=> \(\left(x+\sqrt{3}-1\right)^2=3-2\sqrt{3}\) .Có VP<0 => PT (2) vô nghiệm
Vậy pt (*) có nghiệm x=\(-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\)

\(a,\Leftrightarrow\left(x-2\right)\left(3x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\\ b,\Leftrightarrow\left(x-2\right)^3=0\Leftrightarrow x-2=0\Leftrightarrow x=2\\ c,\Leftrightarrow\left(4x-3x-3\right)\left(4x+3x+3\right)=0\\ \Leftrightarrow\left(x-3\right)\left(7x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{3}{7}\end{matrix}\right.\\ d,\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

a: \(8x\left(x-2017\right)-2x+4034=0\)
\(\Leftrightarrow\left(x-2017\right)\left(8x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2017\\x=\dfrac{1}{4}\end{matrix}\right.\)

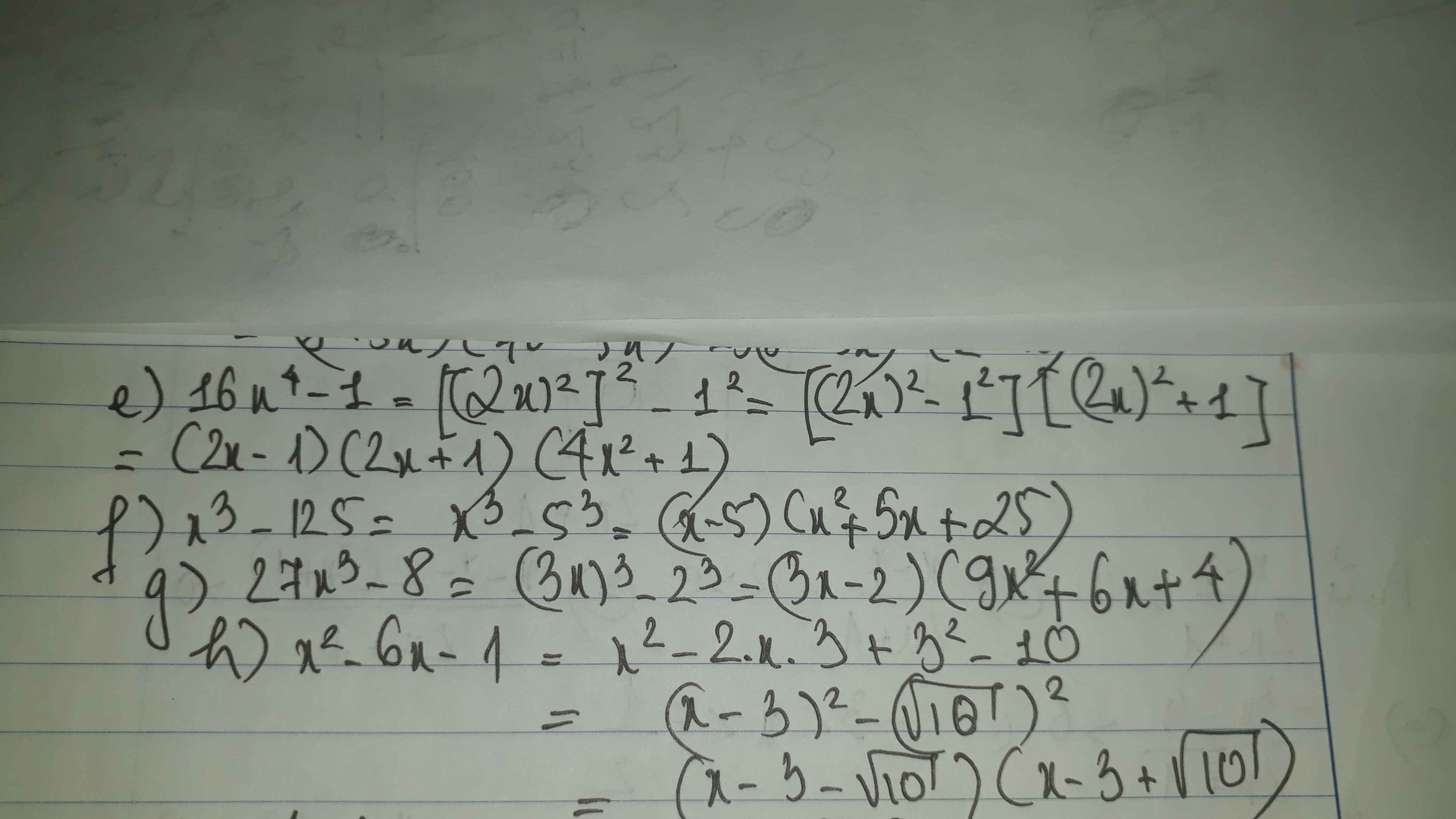
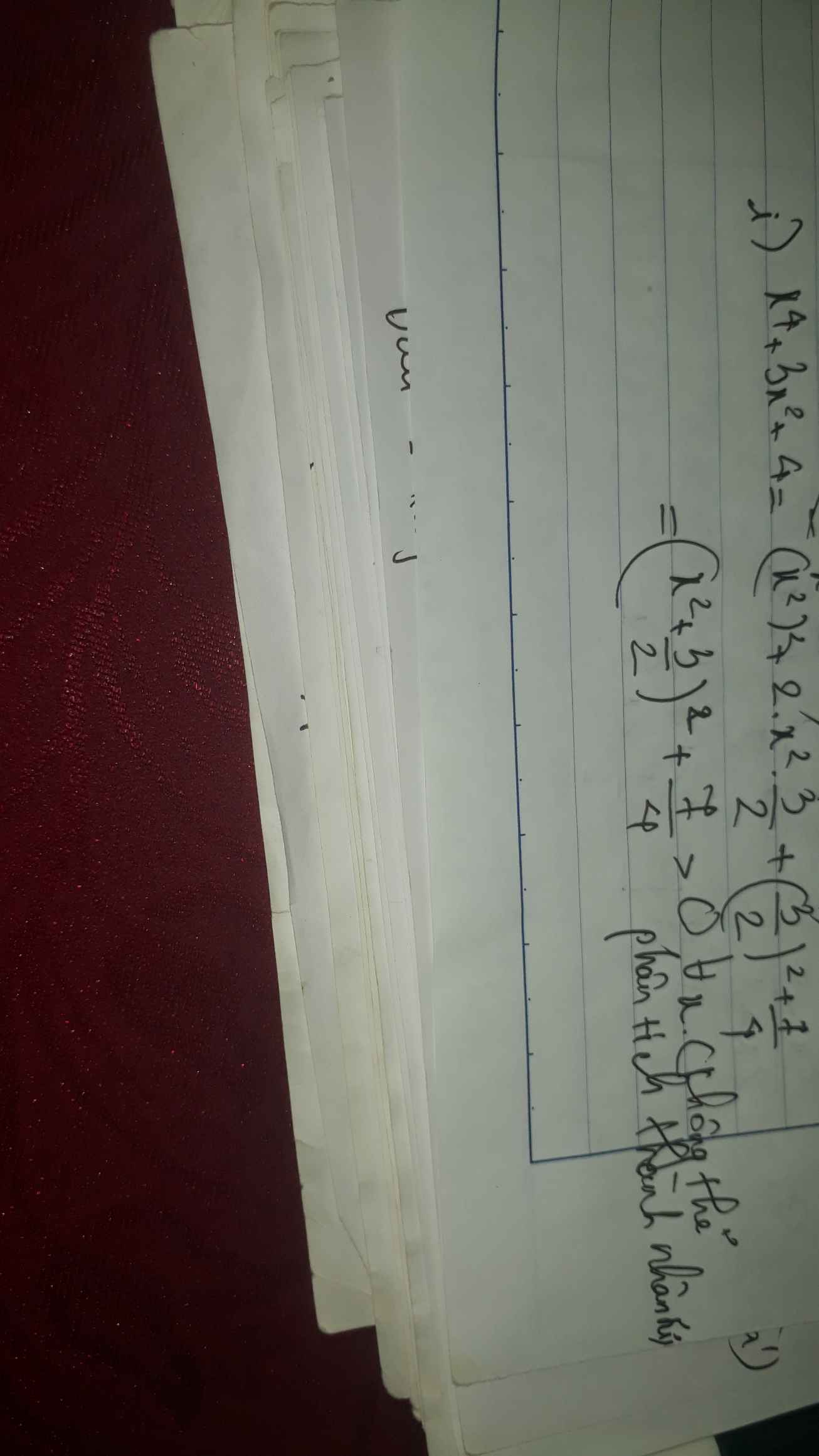
\(7x\left(16x^2-1\right)=0\)
\(\Leftrightarrow7x\left(4x-1\right)\left(4x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
16x^2-1=0
16 x^2=1
x^2=1/16
x=1/4