Cho hai đa thức :
P(x)= x2 + 2mx+m2
Q(x)=x2+(2mx+1)x+m2.
Tìm m biết p(2)=Q(-2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KH
1
14 tháng 3 2017
Ta có:
\(P\left(x\right)=x^2+2mx+m^2\)
\(\Leftrightarrow P\left(1\right)=1+2m+m^2\)
\(Q\left(x\right)=x^2+\left(2m+1\right).x+m^2\)
\(\Leftrightarrow Q\left(-1\right)=1-\left(2m+1\right)+m^2=m^2-2m\)
Mà \(P\left(1\right)=Q\left(-1\right)\)
\(\Leftrightarrow1+2m+m^2=m^2-2m\)
\(\Leftrightarrow2m+2m=-1\)
\(\Leftrightarrow4m=-1\)
\(\Leftrightarrow m=\frac{-1}{4}\)
Vậy \(m=\frac{-1}{4}\)
TA
4 tháng 6 2021
PT có 2 nghiệm phân biệt `<=> \Delta'>0`
`<=>m^2-(m^2+m-5)>0`
`<=>-m+5>0`
`<=> m < 5`
Viet: `x_1+x_2=2m`
`x_1x_2=m^2+m-5`
Theo đề bài: `2(x_1^2+x_2^2)-3x_1x_2=29`
`<=>2[(x_1+x_2)^2-2x_1x_2]-3x_1x_2=29`
`<=>2(x_1+x_2)^2-7x_1x_2=29`
`<=>2.4m^2 - 7(m^2+m-5)=29`
`<=>` \(\left[{}\begin{matrix}m=6\left(L\right)\\m=1\left(TM\right)\end{matrix}\right.\)
Vậy `m=1`.
CM
14 tháng 11 2017
Chọn D
Đặt t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:
t2+ 2(1-m) t+ m2- 3 m+2= 0 (2)
Để pt (1) có nghiệm x≤ 1 khi và chỉ khi pt (2) có nghiệm t≤ 0
TH1: Pt(2) có nghiệm : t1≤ 0 ≤ t2
Khi đó; P= t1.t2 ≤0 hay m2- 3m+ 2≤ 0 hay 1≤ m ≤ 2
TH2: pt (2) có nghiệm
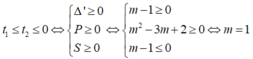
Kết luận: với 1≤ m≤ 2 thì pt (1) có nghiệm x≤1
TT
0
26 tháng 11 2021
\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)
CM
16 tháng 1 2018
Chọn D
Đặt t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:
t2+ 2(1-m) t+ m2- 3 m+2= 0 (2)
Để pt (1) có nghiệm x ≥ 1 khi và chi khi pt (2) có nghiệm t ≥ 0
+ TH1: Pt (2) có nghiệm t1 ≤ 0 ≤ t2
Khi đó; P= t1.t2 ≤ 0 hay m2- 3m+ 2 ≤ 0
Từ đó; 1≤ m≤ 2
+ TH2: Pt (2) có nghiệm :
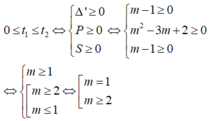
Kết luận: với 
thì pt (1) có nghiệm x ≥ 1
\(P\left(2\right)=2^2+2.m.2+m^2=4+4m+m^2\)
\(Q\left(-2\right)=-2^2+\left[2.m.\left(-2\right)+1\right].\left(-2\right)+m^2=4+8m+m^2\)
Từ đây làm nốt nhé