Giúp t câu d với ạ, cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



d) Gọi x,y lần lượt là số mol Al, Fe
\(\left\{{}\begin{matrix}27x+56y=8,3\\1,5x+y=0,25\end{matrix}\right.\)
=> x=0,1 ; y=0,1
Kết tủa : Al(OH)3, Fe(OH)2
Bảo toàn nguyên tố Al: \(n_{Al\left(OH\right)_3}=n_{Al}=0,1\left(mol\right)\)
Bảo toàn nguyên tố Fe: \(n_{Fe\left(OH\right)_2}=n_{Fe}=0,1\left(mol\right)\)
=> \(m=0,1.78+0,1.90=16,8\left(g\right)\)
Nung kết tủa thu được chất rắn : Al2O3 và FeO
Bảo toàn nguyên tố Al: \(n_{Al_2O_3}.2=n_{Al}\Rightarrow n_{Al_2O_3}=0,05\left(mol\right)\)
Bảo toàn nguyên tố Fe: \(n_{FeO}=n_{Fe}=0,1\left(mol\right)\)
=> \(a=0,05.102+0,1.72=12,3\left(g\right)\)

Câu d có thể liệt kê ra, hoặc làm như sau:
Dễ dàng nhận ra với lần đầu tiên tung ra mặt có số chấm là 1,2,5,6 thì chỉ có 1 khả năng để 2 lần cách nhau 2 chấm là 3,4,3,4
Còn với các chấm 3 và 4 xuất hiện ở lần đầu thì có 2 khả năng tung lần 2 để 2 lần gieo cách nhau 2 chấm
Như vậy n(C) = 4.1 + 2.2 = 8

a: góc ABC=90 độ-góc ACB
góc KHC=90 độ-góc ACB
=>góc ABC=góc KHC
b: Xét ΔBAH vuông tại A và ΔBKH vuông tại K có
BH chung
góc ABH=góc KBH
=>ΔBAH=ΔBKH
=>BA=BK và HA=HK
=>BH là trung trực của AK
c: Xét ΔIBC có
BD,CA là đường cao
BD căt CAt tại H
=>H là trực tâm
=>I,H,K thẳng hàng
d: ΔADK đều
=>góc ADH=30 độ
=>góc AIK=30 độ
=>góc ABC=60 độ


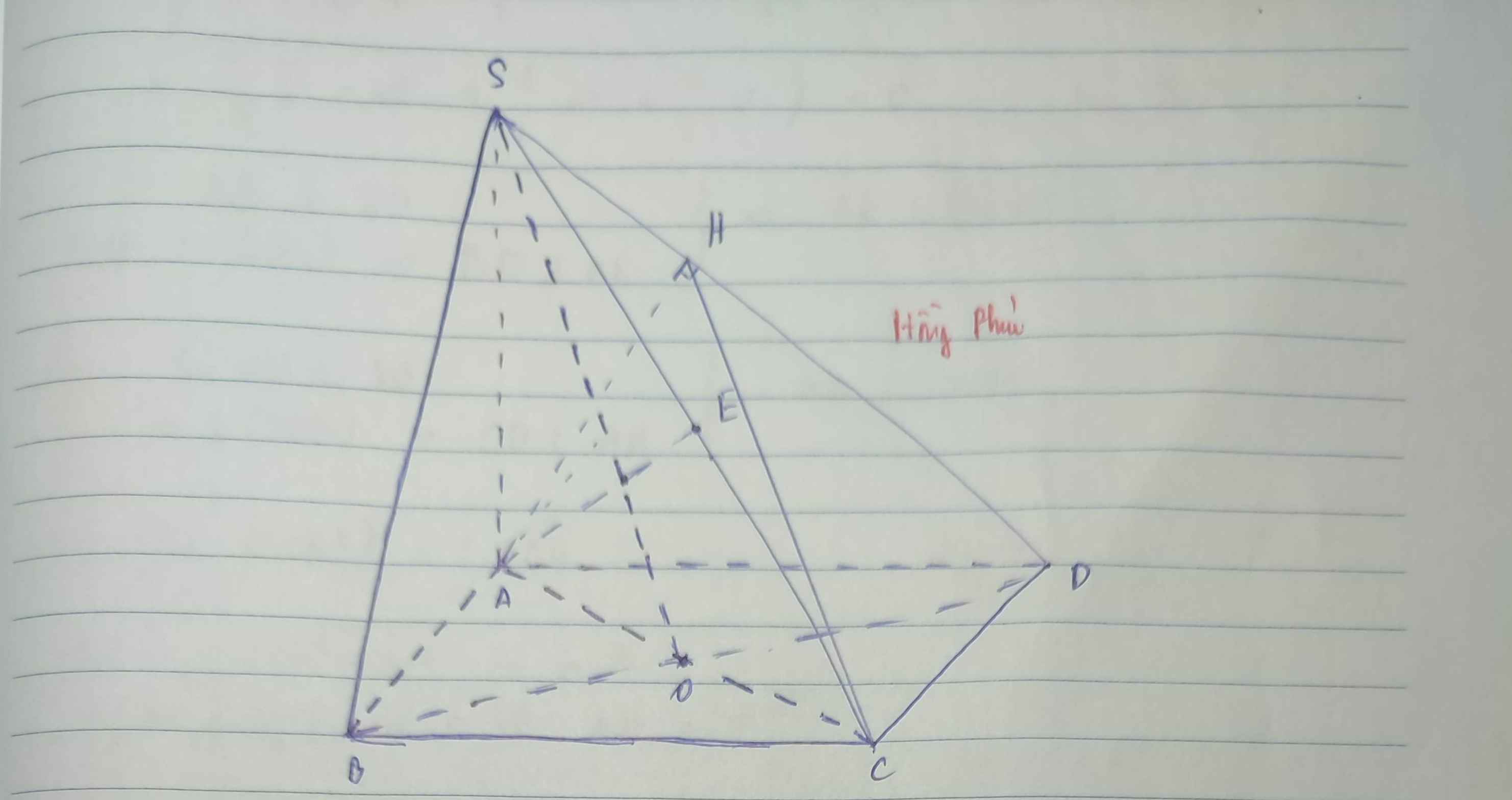

 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 


\(a,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{x-2}=x-2\\ \Leftrightarrow x-2=x^2-4x+4\\ \Leftrightarrow x^2-5x+6=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=3\left(tm\right)\end{matrix}\right.\\ b,ĐK:x\ge5\\ PT\Leftrightarrow x^2-2x+3=x^2-10x+25\\ \Leftrightarrow8x=22\Leftrightarrow x=\dfrac{11}{4}\left(ktm\right)\\ \Leftrightarrow x\in\varnothing\\ c,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow9\left(2x-1\right)=\left(2x-5\right)^2\\ \Leftrightarrow18x-9=4x^2-20x+25\\ \Leftrightarrow4x^2-38x+24=0\\ \Leftrightarrow2x^2-19x+12=0\\ \Delta=361-96=265\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{19-\sqrt{265}}{4}\left(tm\right)\\x=\dfrac{19+\sqrt{265}}{4}\left(tm\right)\end{matrix}\right.\)
\(d,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{\left(\sqrt{x-2}+1\right)^2}=\sqrt{x-2}+1\\ \Leftrightarrow\sqrt{x-2}+1-\sqrt{x-2}-1=0\\ \Leftrightarrow0=0\left(luôn.đúng\right)\Leftrightarrow x\in R;x\ge2\)
\(e,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=2\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=3\\ f,ĐK:x\ge1\\ PT\Leftrightarrow3\sqrt{x-1}-2\sqrt{x-1}+4\sqrt{x-1}-3\sqrt{x-1}=16\\ \Leftrightarrow\sqrt{x-1}=8\\ \Leftrightarrow x-1=64\Leftrightarrow x=65\left(tm\right)\)
Dạ mình cảm ơn ạ