Cho hình thang ABCD (AB // CD). Một đường thẳng song song với AB cắt AD và BC ở E và F. Chứng minh: \(\dfrac{ED}{AD}+\dfrac{BF}{BC}=1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 1
Xét hình thang ABCD có EF//AB//CD
nên \(\dfrac{AE}{ED}=\dfrac{BF}{FC}\)
=>\(\dfrac{ED}{AE}=\dfrac{CF}{FB}\)
=>\(\dfrac{ED+EA}{AE}=\dfrac{CF+FB}{FB}\)
=>\(\dfrac{AD}{AE}=\dfrac{BC}{FB}\)
=>\(\dfrac{AE}{AD}=\dfrac{BF}{BC}\)
=>\(\dfrac{BF}{BC}=1-\dfrac{ED}{AD}\)
=>\(\dfrac{BF}{BC}+\dfrac{ED}{AD}=1\)
16 tháng 2 2021
Gọi O là giao điểm của AC và EF
Xét tam giác ADC có EO //DC
=>AE/AD=AO/AC. (1)
Xét tg ABC có OF//DC
=>CF/CB=CO/CA. (2)
Từ 1 và 2=>AE/AD+CF/CB=AO/AC+CO/CA=AO+CO/AC=AC/AC=1(đpcm)
W
3 tháng 3 2020
Kẻ đoạn thẳng AC nối hai điểm A và C. Gọi O là giao điểm của đoạn thẳng AC và đoạn thẳng EF. Theo đề bài, do EF//AB và EF//CD nên áp dụng định lý Talet trong tam giác, ta có:
Xét tam giác ABC:\(\frac{FC}{FB}=\frac{OC}{OA}\)(1)
Xét tam giác ACD:\(\frac{OC}{OA}=\frac{ED}{AD}\)(2)
Từ (1) và (2), suy ra \(\frac{ED}{AD}=\frac{FC}{BC}\)(đpcm)
3 tháng 3 2020
Gọi giao điểm của AC và EF là O
Xét tam giác ABC có:OF//AB ( EF//AB)
\(\Rightarrow\frac{FC}{BC}=\frac{OC}{AC}\)( định lý Ta-let ) (1)
Xét tam giác ADC có OE//DC ( EF//DC)
\(\Rightarrow\frac{ED}{AD}=\frac{OC}{AC}\)( định lý Ta-let ) (2)
Từ (1) và (2) \(\Rightarrow\frac{FC}{BC}=\frac{ED}{AD}\left(đpcm\right)\)
22 tháng 4 2017
Giải:
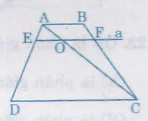
a) Nối AC cắt EF tại O
∆ADC có EO // DC => = (1)
∆ABC có OF // AB => = (2)
Từ 1 và 2 => =
b) Từ = => =
hay =
c) Từ = => =
=>
Gọi I là giao điểm của BD và EF
EI//AB => \(\frac{DE}{AD}=\frac{ID}{DB}\)
IF//DC => \(\frac{BI}{BD}=\frac{BF}{BC}\)
=> \(\frac{DE}{AD}+\frac{BF}{BC}=\frac{ID}{DB}+\frac{BI}{BD}=\frac{BI+ID}{BD}=\frac{BD}{BD}=1\)
Gọi I là giao điểm của DB và EF
Xét tam giác ADB
Có : EI // AB
\(\Rightarrow\frac{DE}{AD}=\frac{ID}{DB}\)( 1 )
Xét tam giác DBC
Có : IF // DC
\(\Rightarrow\frac{BI}{BD}=\frac{BF}{BC}\)( 2 )
Từ (1)(2) , suy ra
\(\frac{DE}{AD}+\frac{BF}{BC}=\frac{ID}{DB}+\frac{BI}{BD}=\frac{BI+ID}{BD}=\frac{BD}{BD}=1\)
Vậy : \(\frac{ED}{AD}+\frac{BF}{BC}=1\)
Em làm kiểu này không biết có đúng không cô Chi check lại giúp em ạ <3