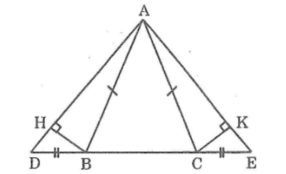
Cho tam giác ABC cân tại A . Trên cạnh AB lấy D . Trên tia đối CA lấy E sao cho BD = CE .Nối D với E ,kẻ DH vuông góc với BC , CK vuông góc BC . Chứng minh :
a) BH=CK
b) BC<DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 1
a: ta có: \(\widehat{KCE}=\widehat{ACB}\)(hai góc đối đỉnh)
\(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
Do đó: \(\widehat{KCE}=\widehat{ABC}\)
Xét ΔDHB vuông tại H và ΔEKC vuông tại K có
BD=CE
\(\widehat{DBH}=\widehat{ECK}\)
Do đó: ΔDHB=ΔEKC
=>BH=CK
7 tháng 7 2023
a: Xét ΔDHB vuông tại H và ΔEKC vuông tại K có
BD=CE
góc DBH=góc ECK
=>ΔDHB=ΔEKC
=>BH=CK
b: Tham khảo:
6 tháng 1 2022
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE và \(\widehat{D}=\widehat{E}\)
Xét ΔHBD vuông tại H và ΔKEC vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔHBD=ΔKCE
Suy ra: BH=CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do dó: ΔABH=ΔACK
13 tháng 2 2022
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K cso
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔBHD=ΔCKE
Suy ra: BH=CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
BH=CK
Do đó: ΔABH=ΔACK
4 tháng 2 2022
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó; ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK
b: Ta có: ΔABH=ΔACK
nên \(\widehat{ABH}=\widehat{ACK}\)
c: Ta có: \(\widehat{OBC}=\widehat{HBD}\)
\(\widehat{OCB}=\widehat{KCE}\)
mà \(\widehat{HBD}=\widehat{KCE}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
CM
17 tháng 5 2018
Vì ΔABC cân tại A nên∠(ABC) =∠(ACB) (tính chất tam giác cân)
Ta có: ∠(ABC) +∠(ABD) =180o(hai góc kề bù)
∠(ACB) +∠(ACE) =180o(hai góc kề bù)
Suy ra: ∠(ABD) =∠(ACE)
Xét ΔABD và ΔACE, ta có:
AB = AC (gt)
∠(ABD) =∠(ACE) (chứng minh trên)
BD=CE (gt)
Suy ra: ΔABD= ΔACE (c.g.c)
⇒∠D =∠E (hai góc tương ứng)
Xét hai tam giác vuông ΔBHD và ΔCKE, ta có:
∠(BHD) =∠(CKE) = 90º
BD=CE (gt)
∠D =∠E (chứng minh trên)
Suy ra: ΔBHD= ΔCKE (cạnh huyền – góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)