tìm bảy số nguyên liên tiếp sao cho tổng bình phương bốn số đầu bằng tổng bình phương ba số sau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi 3 số nguyên liên tiếp là a-1, a, a+1 (a ∈ Z)
Theo đề ta có \(\left(a-1\right)^2+a^2=\left(a+1\right)^2\)
\(\Leftrightarrow a^2-2a+1+a^2=a^2+2a+1\)
\(\Leftrightarrow a^2-4a=0\)
\(\Leftrightarrow a\left(a-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\\a=4\end{matrix}\right.\)
Vậy có 2 cặp 3 số nguyên liên tiếp đó là \(\left(-1;0;1\right)\) và \(\left(3;4;5\right)\)
Tick nha bạn 😘

Đáp án C
Gọi d = 2 x là công sai
ta có bốn số là a - 3 x , a - x , a + x , a + 3 x
Khi đó, từ giả thiết ta có:
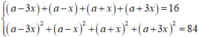
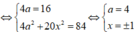
⇔ 1 , 3 , 5 , 7 7 , 5 , 3 , 1
Tổng bình phương của số hạng đầu và cuối là 1 2 + 7 2 = 50

Đáp án C.

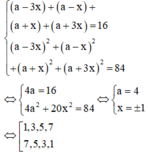
Tổng bình phương của số hạng đầu và cuối là 1 2 + 7 2 = 50

Gọi 3 số nguyên tố liên tiếp cần tìm là p, q, r.
Ta có p2 + q2 + r2 = A là số nguyên tố.
Giả sử p < q < r
Do p, q, r là các số nguyên tố nên A = p2 + q2 + r2 > 3 nên
Nếu p, q, r đều không chia hết cho 3 khi đó p2 ; q2 ;r2 khi chia cho 3 dư 1 hoặc dư 2.
=> A chia hết cho hết cho 3 mà A > 3 nên A là hợp số trái với giả thiết (loại)
Vậy p chia hết cho 3, vì p nguyên tố nên p = 3 \(\Rightarrow\) q = 5 ; r = 7
Khi đó 32 + 52 + 72 = 83 là số nguyên tố
Vậy 3 số nguyên tố cần tìm chỉ có 3 ; 5 ; 7 thỏa mãn.
Đinh Tuấn Việt nhầm rồi:
Sửa lại: p; q;r là số nguyên tố > 3 => chúng có dạng 3k + 1 hoặc 3k + 2
=> p2; q2; r2 chia cho 3 đều dư 1
=> p2 + q2+ r2 chia hết cho 3 => A chia hết cho 3
.....................

Gọi 3 số đó là a - 1 ; a ; 1 + a
Ta có :
\(a^2+\left(a-1\right)^2=\left(a+1\right)^2\)
\(a^2+a^2+1-2a=a^2+1+2a\)
\(a^2-2a=2a\)
\(a^2=4a\)
\(a^2-4a=0\)
\(a\left(a-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}a=0\\a=4\end{cases}}\)
Vậy...

Chọn B
Gọi ba số hạng liên tiếp của cấp số cộng là a - 2x; a ; a+2x với công sai d=2x.
Theo giả thiết ta có:
a − 2 x + a + a + 2 x = − 9 ( a - 2 x ) 2 + a 2 + a + 2 x 2 = 29 ⇔ 3 a = − 9 3 a 2 + 8 x 2 = 29 ⇔ a = − 3 8 x 2 = 2 ⇔ a = − 3 x = ± 1 2
với
x = 1 2 ⇒ u 1 = a − 2 x = − 3 − 2. 1 2 = − 4
với
x = − 1 2 ⇒ u 1 = a − 2 x = − 3 − 2. − 1 2 = − 2
Vậy số hạng đầu tiên là -4 hoặc -2

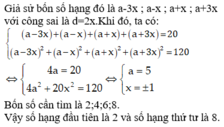
Gọi 7 số nguyên liên tiếp là: n; n+1; n+2; n+3; n+4; n+5; n+6. Theo đề bài
\(n^2+\left(n+1\right)^2+\left(n+2\right)^2+\left(n+3\right)^2=\left(n+4\right)^2+\left(n+5\right)^2+\left(n+6\right)^2.\)
Khai triển, rút gọn rồi giải phương trình bậc 2 để tìm n phù hợp