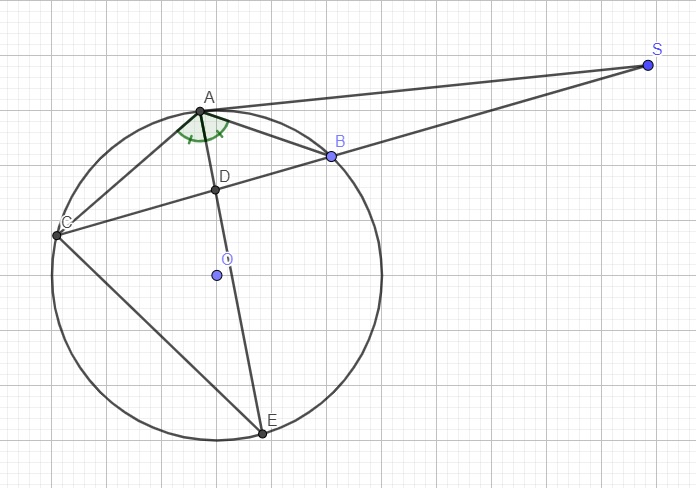
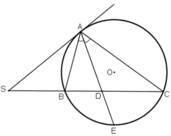
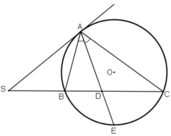
Từ 1 điểm S nằm ngoài đường tròn ( O ) kẻ tiếp tuyến SA và cát tuyết SBC sao cho góc BAC < 90 độ. Tia phân giác của góc BAC cắt dây BC tại D và cắt đường tròn ( O ) tại điểm thứ hai là E. Các tiếp tuyến của đường tròn tại C và E cắt nhau tại N. Gọi Q, P theo thứ tự là giao điểm của các cặp đường thẳng AB và CE, AE và CN....
Đọc tiếp
Từ 1 điểm S nằm ngoài đường tròn ( O ) kẻ tiếp tuyến SA và cát tuyết SBC sao cho góc BAC < 90 độ. Tia phân giác của góc BAC cắt dây BC tại D và cắt đường tròn ( O ) tại điểm thứ hai là E. Các tiếp tuyến của đường tròn tại C và E cắt nhau tại N. Gọi Q, P theo thứ tự là giao điểm của các cặp đường thẳng AB và CE, AE và CN. CMR:
\(\frac{1}{CN}=\frac{1}{CD}+\frac{1}{CP}\)
là góc có đỉnh nằm bên trong đường tròn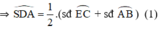
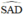là góc tạo bởi tiếp tuyến AS và dây AE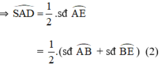
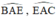lần lượt là các góc nội tiếp chắn các cung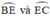 
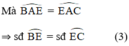
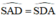
là góc có đỉnh nằm bên trong đường tròn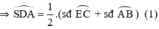
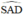là góc tạo bởi tiếp tuyến AS và dây AE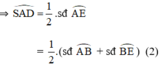
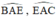lần lượt là các góc nội tiếp chắn các cung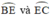 
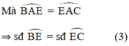
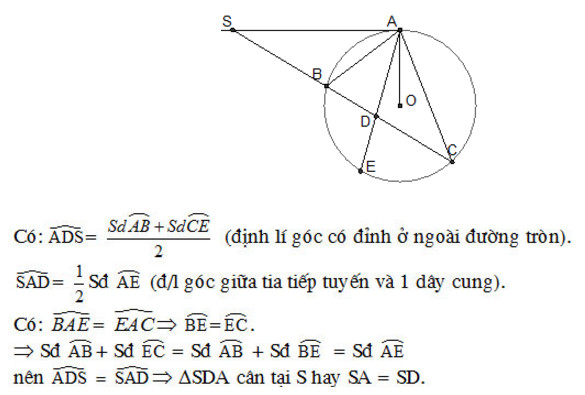
Xét đường tròn (O) có 2 tiếp tuyến NE, NC (E và C là tiếp điểm) => EN = CN (T/c 2 tiếp tuyến giao nhau)
Ta thấy: ^BAC nội tiếp (O), phân giác ^BAC cắt (O) tại điểm thứ hai E => E là điểm chính giữa cung nhỏ BC
=> OE vuông góc với BC. Mà EN vuông góc OE nên EN // BC. Áp dụng ĐL Thales có:
\(\frac{CN}{CD}=\frac{EN}{CD}=\frac{PN}{CP}\)=> \(\frac{CN}{CD}+\frac{CN}{CP}=\frac{PN+CN}{CP}=1\)=> \(\frac{1}{CN}=\frac{1}{CD}+\frac{1}{CP}\)(đpcm).