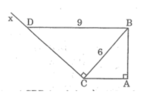
Cho điểm B nằm giữa hai điểm A và C sao cho AB= 4cm, BC= 9cm. Từ điểm B kẻ đường thẳng d vuông góc với AC. Trên đường thẳng d lấy điểm D sao cho BD=6cm. Trên đoạn thẳng BC lấy điểm E sao cho BE= 6cm. Từ E kẻ đường thẳng song song với BD cắt DC tại F. Chứng minh AD=DF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 4 2019
Xét hai tam giác vuông ABC và CDB, ta có:
∠ (BAC) = ∠ (DCB) = 90 0 (1)
Mà: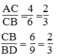
Suy ra: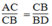 
(2)
Từ (1) và (2) suy ra: △ ABC đồng dạng △ CDB (cạnh huyền và cạnh góc vuông tỉ lệ)
Suy ra: ∠ (ACB) = ∠ (CBD)
⇒ BD//AC ( hai góc ở vị trí so le trong bằng nhau )
28 tháng 10 2023
a: Xét ΔDAC vuông tại A và ΔCBE vuông tại B có
DA=CB
AC=BE
Do đó: ΔDAC=ΔCBE
b: ΔDAC=ΔCBE
=>\(\widehat{DCA}=\widehat{CEB}\)
=>\(\widehat{DCA}+\widehat{ECB}=90^0\)
\(\widehat{DCA}+\widehat{DCE}+\widehat{BCE}=180^0\)(hai góc kề bù)
=>\(\widehat{DCE}+90^0=180^0\)
=>\(\widehat{DCE}=90^0\)
=>CD\(\perp\)CE
CM
12 tháng 11 2019
a) Điểm E nằm giữa hai điểm C, D vì CD = 5cm > CE = 3cm.
b) Trong ba tia BD,BE,BC tia BE nằm giữa hai tia còn lại vì điểm E nằm giữa hai điểm C, D.
c) DE = 2cm.
d) D là trung điểm của đoạn thẳng AE vì AD = DE = 2cm.
e) Đoạn thẳng BD là cạnh, của các tam giác: BDA, BDE,BDC.
DT
9 tháng 4 2019
a, áp dụng định lí py-ta-go ta có:
\(AB^2+AC^2=BC^2\)
=>\(BC^2\)=64+36=100(cm)
=>BC=10cm
vậy BC=10cm
b,xét 2t.giác vuông ABE và DBE có:
EB chung
AB=BD(gt)
=>t.giác ABE=t.giác DBE(cạnh huyền-cạnh góc vuông)
c,xét 2 t.giác vuông AEF và t.giác DEC có:
AE=DE(theo câu b)
\(\widehat{AEF}\)=\(\widehat{DEC}\)(vì đối đỉnh)
=>t.giác AEF=t.giác DEC(cạnh góc vuông-góc nhọn)
=>AF=DC mà BA=BD(gt) suy ra BF=BC
d,gọi O là giao điểm của BE và CF
xét t.giác BFO và t.giác BCO có:
BF=BC(theo câu c)
\(\widehat{FBO}\)=\(\widehat{CBO}\)(theo câu b)
BO cạnh chung
=> t.giác BFO=t.giác BCO(c.g.c)
=>CO=OF =>O là trung điểm của CF(1); \(\widehat{COB}\)=\(\widehat{FOB}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{COB}\)=\(\widehat{FOB}\)=90 độ =>BO\(\perp\)CF(2)
Từ (1) và (2) suy ra BE là trung trực của CF
học tốt!