1.Cho \(S=\left(1-\dfrac{2}{2.3}\right)\left(1-\dfrac{2}{3.4}\right)...\left(1-\dfrac{2}{2020.2021}\right)\) là 1 tích của 2019 chữ số. Tính S 2. Biết a,b là các số nguyên dương thỏa mãn: \(a^2-ab b^9...

BH

Bùi Hiền Thảo

13 tháng 1 2019

1.Cho \(S=\left(1-\dfrac{2}{2.3}\right)\left(1-\dfrac{2}{3.4}\right)...\left(1-\dfrac{2}{2020.2021}\right)\) là 1 tích của 2019 chữ số. Tính S 2. Biết a,b là các số nguyên dương thỏa mãn: \(a^2-ab+b^9⋮9\). CMR: cả a và b đều chia hết cho 3 3. Tìm các số nguyên dương n sao cho: 9n+11 là tích của k (\(k\in N,k\ge2\)) số tự nhiên liên...

Đọc tiếp

#Toán lớp 9

1

BH

Bùi Hiền Thảo

13 tháng 1 2019

Bài 2 tớ nhầm nhé, là b²

Đúng(0)

VN

VUX NA

21 tháng 8 2021

Cho a,b,c là cái số thực dương thỏa mãn a + b + c = 1 . Tìm giá trị nhỏ nhất của biểu thức : Q = \(\dfrac{\left(1-c\right)^2}{\sqrt{2\left(b+c\right)^2+bc}}+\dfrac{\left(1-a\right)^2}{\sqrt{2\left(c+a\right)^2+ca}}\) + \(\dfrac{\left(1-b\right)^2}{\sqrt{2\left(a+b\right)^2+ab}}\)

#Toán lớp 9

1

NV

Nguyễn Việt Lâm

Giáo viên

21 tháng 8 2021

\(Q=\sum\dfrac{\left(a+b\right)^2}{\sqrt{2\left(b+c\right)^2+bc}}\ge\sum\dfrac{\left(a+b\right)^2}{\sqrt{2\left(b+c\right)^2+\dfrac{1}{4}\left(b+c\right)^2}}=\dfrac{2}{3}\sum\dfrac{\left(a+b\right)^2}{b+c}\)

\(Q\ge\dfrac{2}{3}.\dfrac{\left(a+b+b+c+c+a\right)^2}{a+b+b+c+c+a}=\dfrac{4}{3}\left(a+b+c\right)=\dfrac{4}{3}\)

Đúng(0)

VN

VUX NA

21 tháng 8 2021

∑ cái này nghĩa là gì ạ

Đúng(0)

C

Cplusplus

14 tháng 1 2021

cho biết tập hợp các giá trị của tham số để phương trình \(2\left(x^2+\dfrac{1}{x^2}\right)-3\left(x+\dfrac{1}{x}\right)-2m-1=0\)

có nghiệm là S = \(\left[\dfrac{-b}{a};+\infty\right]\)

với a, b là các số nguyên dương a/b là phân số tối giản. Tính a + b

#Toán lớp 10

0

MT

Mai Tiến Đỗ

22 tháng 1 2021

Cho a,b,c là các số thực dương thỏa mãn a+b+c=3. Tìm giá trị nhỏ nhất của biểu thức:

\(P=\dfrac{1}{a\left(b^2+bc+c^2\right)}+\dfrac{1}{b\left(c^2+ca+a^2\right)}+\dfrac{1}{c\left(a^2+ab+b^2\right)}+\dfrac{abc}{ab+bc+ca}\)

#Toán lớp 9

1

NV

Nguyễn Việt Lâm

Giáo viên

23 tháng 1 2021

\(abc\ge\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\)

\(\Leftrightarrow abc\ge\left(3-2a\right)\left(3-2b\right)\left(3-2c\right)\)

\(\Leftrightarrow9abc\ge12\left(ab+bc+ca\right)-27\)

\(\Rightarrow abc\ge\dfrac{4}{3}\left(ab+bc+ca\right)-3\)

\(P\ge\dfrac{9}{a\left(b^2+bc+c^2\right)+b\left(c^2+ca+a^2\right)+c\left(a^2+ab+b^2\right)}+\dfrac{abc}{ab+bc+ca}=\dfrac{9}{\left(ab+bc+ca\right)\left(a+b+c\right)}+\dfrac{abc}{ab+bc+ca}\)

\(\Rightarrow P\ge\dfrac{3}{ab+bc+ca}+\dfrac{abc}{ab+bc+ca}=\dfrac{3+abc}{ab+bc+ca}\)

\(\Rightarrow P\ge\dfrac{3+\dfrac{4}{3}\left(ab+bc+ca\right)-3}{ab+bc+ca}=\dfrac{4}{3}\)

Dấu "=" xảy ra khi \(a=b=c=1\)

Đúng(3)

PK

Phạm Kim Oanh

1 tháng 4 2022

Cho các số thực dương : \(a;b;c\) thỏa mãn điều kiện : \(ab+bc+ac+abc=4\)Chứng minh rằng : \(\dfrac{1}{\sqrt{2.\left(a^2+b^2\right)}+4}+\dfrac{1}{\sqrt{2.\left(b^2+c^2\right)}+4}+\dfrac{1}{\sqrt{2.\left(c^2+a^2\right)}+4}\le\dfrac{1}{2}\)P/s: Em xin phép nhờ sự giúp đỡ của quý thầy cô giáo và các bạn yêu toán. Em cám ơn nhiều lắm...

Đọc tiếp

#Toán lớp 10

1

KB

Khôi Bùi

2 tháng 4 2022

Dễ dàng c/m : \(\dfrac{1}{a+2}+\dfrac{1}{b+2}+\dfrac{1}{c+2}=1\)

Ta có : \(\dfrac{1}{\sqrt{2\left(a^2+b^2\right)}+4}\le\dfrac{1}{a+b+4}\le\dfrac{1}{4}\left(\dfrac{1}{a+2}+\dfrac{1}{b+2}\right)\)

Suy ra : \(\Sigma\dfrac{1}{\sqrt{2\left(a^2+b^2\right)}+4}\le2.\dfrac{1}{4}\left(\dfrac{1}{a+2}+\dfrac{1}{b+2}+\dfrac{1}{c+2}\right)=\dfrac{1}{2}.1=\dfrac{1}{2}\)

" = " \(\Leftrightarrow a=b=c=1\)

Đúng(3)

PK

Phạm Kim Oanh

2 tháng 4 2022

Dạ em cám ơn nhiều lắm ạ

Đúng(0)

G

Gallavich

16 tháng 4 2021

Cho a,b,c là các số thực dương thỏa mãn điều kiện abc=1

Chứng minh rằng : \(P=\dfrac{1}{\left(a+1\right)^2}+\dfrac{1}{\left(b+1\right)^2}+\dfrac{1}{\left(c+1\right)^2}+\dfrac{2}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}\ge1\)

#Toán lớp 8

1

NV

Nguyễn Việt Lâm

Giáo viên

17 tháng 4 2021

Theo nguyên lý Dirichlet, trong 3 số a;b;c luôn có ít nhất 2 số cùng phía so với 1

Không mất tính tổng quát, giả sử đó là a và b

\(\Rightarrow\left(a-1\right)\left(b-1\right)\ge0\)

\(\Leftrightarrow ab+1\ge a+b\)

\(\Leftrightarrow2\left(ab+1\right)\ge\left(a+1\right)\left(b+1\right)\)

\(\Rightarrow\dfrac{2}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}\ge\dfrac{2}{2\left(ab+1\right)\left(c+1\right)}=\dfrac{1}{\left(ab+1\right)\left(c+1\right)}=\dfrac{1}{\left(\dfrac{1}{c}+1\right)\left(c+1\right)}=\dfrac{c}{\left(c+1\right)^2}\)

Lại có:

\(\dfrac{1}{\left(\sqrt{ab}.\sqrt{\dfrac{a}{b}}+1.1\right)^2}+\dfrac{1}{\left(\sqrt{ab}.\sqrt{\dfrac{b}{a}}+1\right)^2}\ge\dfrac{1}{\left(ab+1\right)\left(\dfrac{a}{b}+1\right)}+\dfrac{1}{\left(ab+1\right)\left(\dfrac{b}{a}+1\right)}=\dfrac{1}{ab+1}\)

\(\Rightarrow P\ge\dfrac{1}{ab+1}+\dfrac{1}{\left(c+1\right)^2}+\dfrac{c}{\left(c+1\right)^2}=\dfrac{1}{\dfrac{1}{c}+1}+\dfrac{1}{\left(c+1\right)^2}+\dfrac{c}{\left(c+1\right)^2}\)

\(\Rightarrow P\ge\dfrac{c}{c+1}+\dfrac{c+1}{\left(c+1\right)^2}=\dfrac{c\left(c+1\right)+c+1}{\left(c+1\right)^2}=\dfrac{\left(c+1\right)^2}{\left(c+1\right)^2}=1\) (đpcm)

Dấu "=" xảy ra khi \(a=b=c=1\)

Đúng(2)

G

Gallavich

17 tháng 4 2021

Em cảm ơn ạ

Đúng(0)

DT

Đào Thu Hoà

15 tháng 1 2019 - olm

1)Giải phương trình

\(\sqrt[3]{2-x}=1-\sqrt{x-1}.\)

2)Cho \(S=\left(1-\frac{2}{2.3}\right)\left(1-\frac{2}{3.4}\right)...\left(1-\frac{2}{2020.2021}\right)\)là một tích của 2019 thừa số. Tính S.

#Toán lớp 9

2

I

Incursion_03

15 tháng 1 2019

\(a,ĐKXĐ:x-1\ge0\Leftrightarrow x\ge1\)

Đặt \(\hept{\begin{cases}\sqrt[3]{2-x}=a\\\sqrt{x-1}=b\left(b\ge0\right)\end{cases}\Rightarrow}a^3+b^2=2-x+x-1=1\)

Lại có: \(a=1-b\)

Thay vào được

\(\left(1-b\right)^3+b^2=1\)

\(\Leftrightarrow1-3b+3b^2-b^3+b^2-1=0\)

\(\Leftrightarrow-b^3+4b^2-3b=0\)

\(\Leftrightarrow b^3-4b^2+3b=0\)

\(\Leftrightarrow b\left(b^2-4b+3\right)=0\)

\(\Leftrightarrow b\left(b-1\right)\left(b-3\right)=0\)

\(\Leftrightarrow b=0\left(h\right)b=1\left(h\right)b=3\)(T/m ĐK b>0)

*Với b = 0

\(\Leftrightarrow\sqrt{x-1}=0\)

\(\Leftrightarrow x=1\left(TmĐKXĐ\right)\)

*Với b = 1

\(\Leftrightarrow\sqrt{x-1}=1\)

\(\Leftrightarrow x-1=1\)

\(\Leftrightarrow x=2\left(TmĐKXĐ\right)\)

*Với b = 3

\(\Leftrightarrow\sqrt{x-1}=3\)

\(\Leftrightarrow x-1=9\)

\(\Leftrightarrow x=10\)

Vậy \(S\in\left\{1;2;10\right\}\)

Đúng(0)

ZC

zZz Cool Kid_new zZz

15 tháng 1 2019

em chỉ bt bài 2 nha!

\(A=\left(1-\frac{2}{2\cdot3}\right)\left(1-\frac{2}{3\cdot4}\right)...\left(1-\frac{2}{2020\cdot2021}\right)\)

\(\frac{2}{3}\cdot\frac{5}{6}\cdot\frac{9}{10}\cdot...\cdot\frac{2020\cdot2021-2}{2020\cdot2021}\left(1\right)\)

Mặt khác:\(2020\cdot2021-2=2020\left(2022-1\right)+2020-2022\)

\(=2020\cdot2022-2022\)

\(=2022\left(2020-1\right)=2019\cdot2022\left(2\right)\)

Từ (1),(2) ta có:

\(A=\frac{4\cdot1}{2\cdot3}\cdot\frac{5\cdot2}{3\cdot4}\cdot...\cdot\frac{2022\cdot2019}{2020\cdot2021}\)

\(=\frac{\left(4\cdot5\cdot6\cdot...\cdot2022\right)\left(1\cdot2\cdot3\cdot...\cdot2019\right)}{\left(2\cdot3\cdot4\cdot...\cdot2020\right)\left(3\cdot4\cdot5\cdot...\cdot2021\right)}\)

\(=\frac{2021\cdot2022}{2\cdot3}\cdot\frac{1\cdot2}{2020\cdot2021}=\frac{2022}{3\cdot2020}=\frac{2022}{6060}\)

Đúng(0)

NM

Nguyễn Minh Anh

15 tháng 3 2022

Cho a, b là các số dương thỏa mãn a + b = 3. CMR

\(\left(a+\dfrac{1}{b}\right)^2+\left(b+\dfrac{1}{a}\right)^2\ge\dfrac{169}{18}\)

#Toán lớp 9

2

D

Dark_Hole

15 tháng 3 2022

:v

Đúng(0)

NM

Nguyễn Minh Anh

15 tháng 3 2022

gie

Đúng(0)

MH

Minh Hiếu

24 tháng 1 2022

1. Phân tích đa thức thành nhân tử:\(x^5-x^4+\left(y+2\right)x^3+\left(y-2\right)x^2+yx+y^2\)2. Cho các số dương thỏa mãn:\(\dfrac{b+c}{a^2}+\dfrac{c+a}{b^2}+\dfrac{a+b}{c^2}=2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\)Tính giá trị biểu thức sau: \(P=\left(a-b\right)^{2009}+\left(b-c\right)^{2009}+\left(c-a\right)^{2009}\)3. Cho x,y,x đôi một khác nhau và khác 0. Chứng minh rằng nếu:\(\dfrac{x^2-yz}{a}=\dfrac{y^2-xz}{b}=\dfrac{z^2-xy}{c}\) thì ta...

Đọc tiếp

#Toán lớp 9

3

S

Sun ...

24 tháng 1 2022

k làm đc k cần phải ghi zậy mô ha

Đúng(0)

NV

Nguyễn Việt Lâm

Giáo viên

24 tháng 1 2022

1.

\(y^2+y\left(x^3+x^2+x\right)+x^5-x^4+2x^3-2x^2\)

\(\Delta=\left(x^3+x^2+x\right)^2-4\left(x^5-x^4+2x^3-2x^2\right)\)

\(=\left(x^3-x^2+3x\right)^2\)

\(\Rightarrow\left[{}\begin{matrix}y=\dfrac{-x^3-x^2-x+x^3-x^2+3x}{2}=-x^2+x\\y=\dfrac{-x^3-x^2-x-x^3+x^2-3x}{2}=-x^3-2x\end{matrix}\right.\)

Hay đa thức trên có thể phân tích thành:

\(\left(x^2-x+y\right)\left(x^3+2x+y\right)\)

Dựa vào đó em tự tách cho phù hợp

Đúng(1)

PK

Phạm Kim Oanh

18 tháng 2 2022

Cho \(a;b;c\) là các số thực dương thỏa mãn :\(0 a;b;c 1\). Chứng minh rằng:\(\dfrac{1}{a.\left(1-b\right)}+\dfrac{1}{b.\left(1-c\right)}+\dfrac{1}{c.\left(1-a\right)}\ge\dfrac{3}{1-\left(a+b+c\right)+ab+bc+ac}\) P/s: Đề cương toán lớp 10 trường THPT chuyên sư phạm Hà Nội.Em xin nhờ quý thầy cô giáo và các bạn giúp đỡ, em cám ơn nhiều...

Đọc tiếp

#Toán lớp 10

1

NV

Nguyễn Việt Lâm

Giáo viên

18 tháng 2 2022

Đặt \(a\left(1-b\right)=x;b\left(1-c\right)=y;c\left(1-a\right)=x\)

\(\Rightarrow1-\left(a+b+c\right)+ab+bc+ca=1-a\left(1-b\right)-b\left(1-c\right)-c\left(1-a\right)=1-x-y-z\)

BĐT cần c/m trở thành:

\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\ge\dfrac{3}{1-x-y-z}\)

\(\Leftrightarrow\left(1-x-y-z\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)-3\ge0\)

\(\Leftrightarrow\dfrac{1-x-y-z}{x}+\dfrac{1-x-y-z}{y}+\dfrac{1-x-y-z}{z}-3\ge0\)

\(\Leftrightarrow\dfrac{1-y-z}{x}+\dfrac{1-z-x}{y}+\dfrac{1-x-y}{z}-6\ge0\) (1)

Lại có: \(1-y-z=1-b\left(1-c\right)-c\left(1-a\right)=1-b-c+bc+ca=\left(1-b\right)\left(1-c\right)+ca\)

Nên (1) tương đương:

\(\dfrac{\left(1-b\right)\left(1-c\right)+ca}{a\left(1-b\right)}+\dfrac{\left(1-a\right)\left(1-c\right)+ab}{b\left(1-c\right)}+\dfrac{\left(1-a\right)\left(1-b\right)+bc}{c\left(1-a\right)}-6\ge0\)

\(\Leftrightarrow\dfrac{1-c}{a}+\dfrac{c}{1-b}+\dfrac{1-a}{b}+\dfrac{a}{1-c}+\dfrac{1-b}{c}+\dfrac{b}{1-a}\ge6\)

BĐT trên hiển nhiên đúng theo AM-GM do:

\(\dfrac{1-c}{a}+\dfrac{c}{1-b}+\dfrac{1-a}{b}+\dfrac{a}{1-c}+\dfrac{1-b}{c}+\dfrac{b}{1-a}\ge6\sqrt[6]{\dfrac{abc\left(1-a\right)\left(1-b\right)\left(1-c\right)}{abc\left(1-a\right)\left(1-b\right)\left(1-c\right)}}=6\) (đpcm)

Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{2}\)

Đúng(2)

PK

Phạm Kim Oanh

19 tháng 2 2022

Cám ơn bài giải của thầy Lâm ạ!
Và từ bài bất đăng thức này, đã được chế thành bài toán hình học trong 1 kì thi học sinh giỏi toán cấp tỉnh thầy ạ!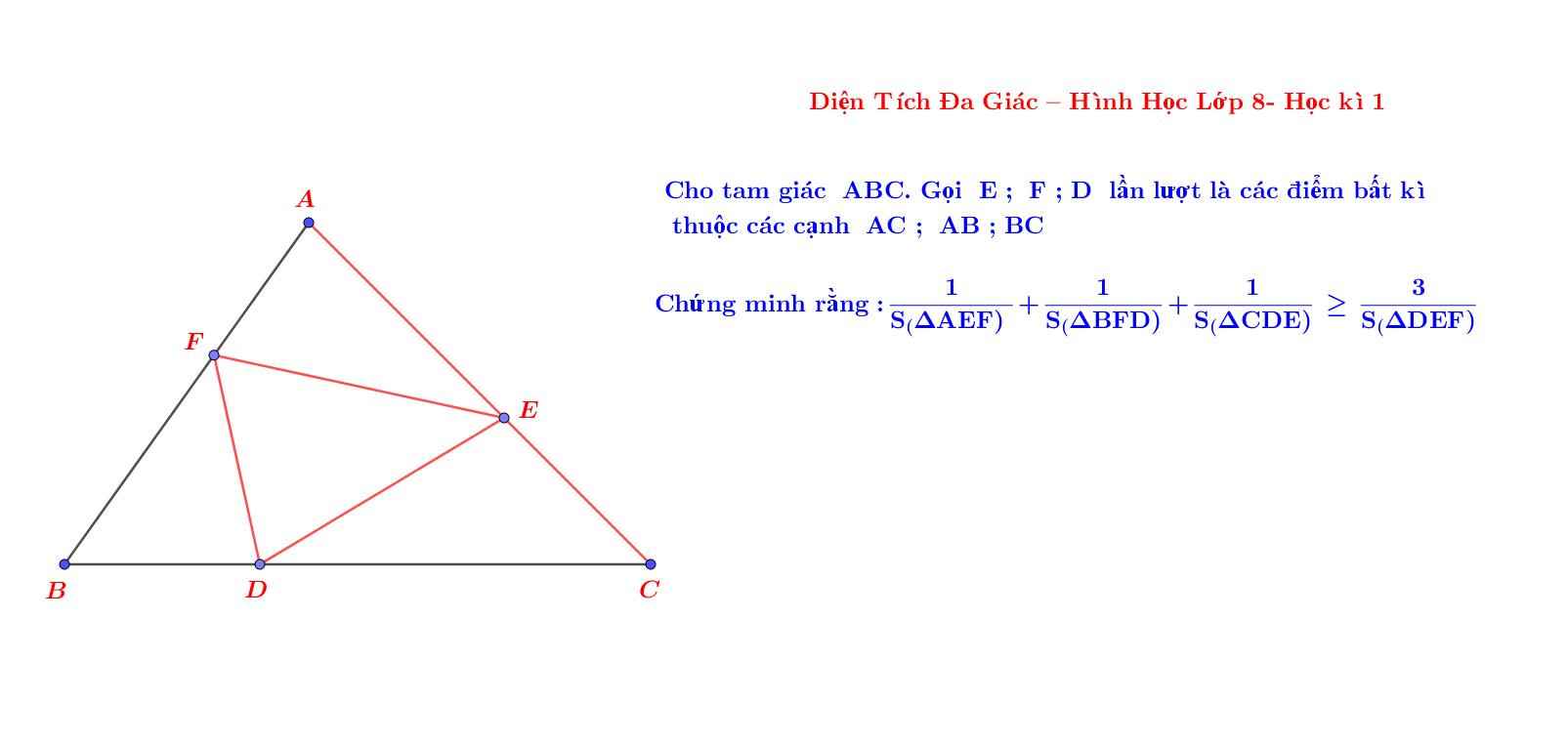 undefined

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP