cho AB=4cm,CD =2,5 cm và MN + EF= 39 cm.Tìm MN và EF biết AB,CD tỉ lệ với MN,EF (áp dụng đoạn thẳng tỉ lệ của định lý Talét).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để AB và CD tỉ lệ với PQ và EF thì \(\dfrac{6}{8}=\dfrac{4}{x}\)
=>\(x=4\cdot\dfrac{8}{6}=\dfrac{32}{6}=\dfrac{16}{3}\left(cm\right)\)

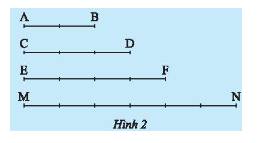
Ta coi mỗi vạch chia là 1 đơn vị. Do đó, độ dài các đoạn thẳng là \(AB = 2\) đơn vị; \(CD = 3\) đơn vị; \(EF = 4\) đơn vị; \(MN = 6\) đơn vị.
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{2}{3}\).
Tỉ số giữa hai đoạn thẳng \(EF\) và \(MN\) là \(EF:MN = \frac{{EF}}{{MN}} = \frac{4}{6} = \frac{2}{3}\).
Do đó, tỉ số của hai đoạn thẳng \(AB\) và \(CD\) bằng tỉ số của hai đoạn thẳng \(EF\) và \(MN\) .

Ta có: AB/CD = MN/PQ ⇔ 8/6 = 12/x ⇔ x = 72/8 = 9cm
Chọn đáp án B.

Ta có:
AB/CD = MN/ PQ ⇔ 8/ 6 = 12/x ⇔ x = 72/8 = 9cm
Chọn đáp án B.