Question

[Trịnh Ngọc Ánh]

Giúp e vs ạ:(

Answer 1

[Nguyễn Huy Tú]

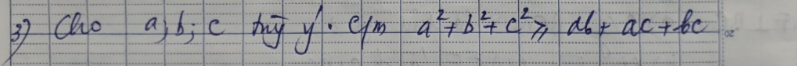
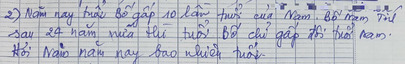
\(A=\left(\frac{2\sqrt{x}+1}{x-1}-\frac{1}{\sqrt{x}+1}\right):\frac{1}{\sqrt{x}-1}\)ĐK : \(x\ge0;x\ne1\)

\(=\left(\frac{2\sqrt{x}+1-\left(\sqrt{x}-1\right)}{x-1}\right):\frac{1}{\sqrt{x}-1}\)

\(=\frac{\sqrt{x}+2}{x-1}:\frac{1}{\sqrt{x}-1}=\frac{\sqrt{x}+2}{\sqrt{x}+1}\)

\(B=\frac{\sqrt{x}}{\sqrt{x}+1}+\frac{1-\sqrt{x}}{\sqrt{x}-2}-\frac{\sqrt{x}+4}{x-\sqrt{x}-2}\)ĐK : \(x\ge0;x\ne4\)

\(=\frac{\sqrt{x}\left(\sqrt{x}-2\right)+\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)-\sqrt{x}-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\)

\(=\frac{x-2\sqrt{x}+1-x-\sqrt{x}-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}==\frac{-3}{\sqrt{x}-2}\)

Answer 2

[Hoàng Mai Trà]

A =( \(\frac{2\sqrt{x}+1}{x-1}\)\(-\) \(\frac{1}{\sqrt{x}+1}\)) \(\div\) \(\frac{1}{\sqrt{x}-1}\)ĐK: x\(\ge0\)và x\(\ne1\)

   =(\(\frac{2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)\(-\)\(\frac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)) \(\div\)\(\frac{1}{\sqrt{x}-1}\)

   =\(\frac{2\sqrt{x}+1-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)\(\times\)\(\frac{\sqrt{x}-1}{1}\)

   =\(\frac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)\(\times\)\(\frac{\sqrt{x}-1}{1}\)

   =\(\frac{\sqrt{x}+2}{\sqrt{x}+1}\)

Vậy A = \(\frac{\sqrt{x}+2}{\sqrt{x}+1}\)với x\(\ge0\)và x\(\ne1\)