Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath
a) Xét tam giác ADB và AEC có:
AD = AE (gt)
AB = AC (gt)
Góc A chung
\(\Rightarrow\Delta ADB=\Delta AEC\left(c-g-c\right)\Rightarrow BD=CE\)
b) Do AB = AC; AD = AE nên BE = DC
Xét tam giác CEB và BDC có:
CE = BD (cma)
Cạnh BC chung
BC = CD (cmt)
\(\Rightarrow\Delta CEB=\Delta BDC\left(c-c-c\right)\)
c) Do \(\Delta ADB=\Delta AEC\Rightarrow\widehat{EBI}=\widehat{DCI}\)
Do \(\Delta CEB=\Delta BDC\Rightarrow\widehat{BEI}=\widehat{CDI}\)
Xét tam giác BIE và tam giác CID có:
\(\widehat{EBI}=\widehat{DCI}\)
\(\widehat{BEI}=\widehat{CDI}\)
BE = CD
\(\Rightarrow\Delta BIE=\Delta CID\left(g-c-g\right)\)
d) Do \(\Delta BIE=\Delta CID\Rightarrow IB=IC\)
Lại có AB = AC nên IA là trung trực của BC
Vậy IA đi qua trung điểm F của BC hay A, I, F thẳng hàng.
Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath
a) Xét ΔADB và ΔAEC có:
AB=AC(gt)
A: chung
AD=AE(gt)
=>ΔADB=ΔAEC(c.g.c)
=>đpcm
b) Có: AB=AC
=>ΔABC cân ở A
=>ABC=ACB(t/c Δ cân)
=>ABD+DBC=ACE+ECB
Mà ABD=ACE(ΔADB=ΔAEC)
=>DBC=ECB
=>ΔBCF cân ở F
=>BF=CF(t/c Δ cân)
c) Ta có:
AB=AE+EB
AC=AD+DC
Mà AB=AC; AE=AD
=>EB=DC
Xét ΔEBC và ΔDCB có:
EB=DC(cmt)
EBC=DCB(ΔABC cân)
BC: chung
=>ΔEBC=ΔDCB(c.g.c)
=>CEB=BDC(hai cạnh tương ứng)
Mà AEC+BEC=ADB+CDB=180°
=>AEC=ADB
Ta có:
EC=EF+FC
BD=BF+FD
Mà EC=BD(ΔEBC=ΔDCB); BF=CF(cmt)
=>FE=FD
Xét ΔAFE và ΔAFD có:
AE=AD(gt)
AEF=ADF(cmt)
FE=FD(cmt)
=>ΔAFE=ΔAFD(c.g.c)
=>EAF=DAF(hai góc tương ứng)
=>AF là pg BAC(1)
Xét ΔHAB và ΔHAC có:
ABH=ACHF(ΔABC cân)
HB=HC(H là trđ BC)
BAH=CAH(cmt)
=>ΔHAB=ΔHAC(g.c.g)
=>BAH=CAH(hai góc tương ứng)
=>AH là pg BAC(2)
Từ (1) và (2)
=>A, F, H thuộc thẳng hàng
a) Xét tam giác ABD: AB = AD (gt).
=> Tam giác ABD cân tại A.
Mà AH là phân giác góc BAD (gt).
=> AH là trung tuyến (Tính chất tam giác cân).
=> H là trung điểm của cạnh BD (đpcm).
a: Ta có: ΔABD cân tại A
mà AH là đường phân giác
nên H là trung điểm của BD
b: Xét ΔABF và ΔADF có
AB=AD
\(\widehat{BAF}=\widehat{DAF}\)
AF chung
Do đó: ΔABF=ΔADF
Suy ra: FB=FD
Xét ΔBFE và ΔDFC có
FB=FD
\(\widehat{FBE}=\widehat{FDC}\)
BE=DC
Do đó: ΔBFE=ΔDFC
Suy ra: \(\widehat{BFE}=\widehat{DFC}\)
mà \(\widehat{DFC}+\widehat{DFB}=180^0\)
nên \(\widehat{BFE}+\widehat{BFD}=180^0\)
=>D,E,F thẳng hàng
a: Ta có: ΔABD cân tại A
mà AH là đường phân giác
nên H là trung điểm của BD
b: Xét ΔABF và ΔADF có
AB=AD
\(\widehat{BAF}=\widehat{DAF}\)
AF chung
Do đó: ΔABF=ΔADF
Suy ra: FB=FD
Xét ΔBFE và ΔDFC có
FB=FD
\(\widehat{FBE}=\widehat{FDC}\)
BE=DC
Do đó: ΔBFE=ΔDFC
Suy ra: \(\widehat{BFE}=\widehat{DFC}\)
mà \(\widehat{DFC}+\widehat{DFB}=180^0\)
nên \(\widehat{BFE}+\widehat{BFD}=180^0\)
=>D,E,F thẳng hàng
Bài này easy lắm bạn
a) Xét \(\Delta\) ABD và \(\Delta\)ACE có
AB = AC ( gt)
\(\widehat{BAC}\) : góc chung
AD = AE ( gt)
=> \(\Delta\)ABD = \(\Delta\) ACE (c-g-c)
=> BD = CE ( 2 cạnh tương ứng )
+) Ta có \(\hept{\begin{cases}AB=AC\left(gt\right)\\AE=AD\left(cmt\right)\end{cases}}\)
\(\Rightarrow AB-AE=AC-AD\)
\(\Rightarrow\)BE = CD
+) Xét \(\Delta\)CEB và \(\Delta\)BDC có
CE = BD ( cmt)
EB = DC ( cmt)
CB: cạnh chung
=> \(\Delta\)CEB = \(\Delta\) BDC (c-c-c)
2 câu này đã nhé
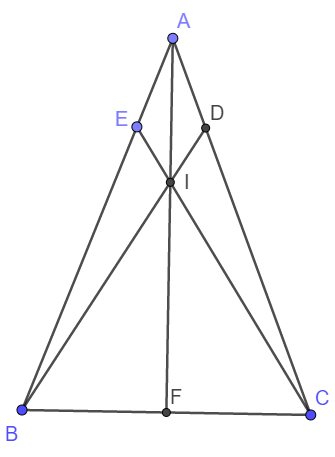
a, Xét Δ ADB và Δ AEC có :
AE = AD ( gt )
AB = AC ( gt )
\(\widehat{A}\) là góc chung
=> Δ ADB = Δ AEC ( c - g -c )
b, Do Δ ABD = Δ AEC (cm trên )
=> BF = CF ( hai cạnh tương ứng )
c, DO Δ ABD = Δ AEC (cm trên )
=> \(\widehat{BAF} = \widehat{CAF}\) ( hai góc tương ứng )
=> AH là tia phân giác \(\widehat{BAC}\)
Xét Δ BFH và Δ CFH có :
FH là cạnh chung
BF = CF ( cm trên )
BH = CH ( do H là trung điểm BC)
=> Δ BFH = Δ CFH ( c - c - c )
=> \(\widehat{BFH} = \widehat{CFH}\) ( hai góc tương ứng )
=> AH là tia phân giác \(\widehat{BFH}\)
mà AH cũng là tia phân giác \(\widehat{BAC}\) ( cm trên )
=> ba điểm A,F,H thẳng hàng
uk