giải, vẽ hình giúp e ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))
1
25 tháng 10 2023
10: Chọn B
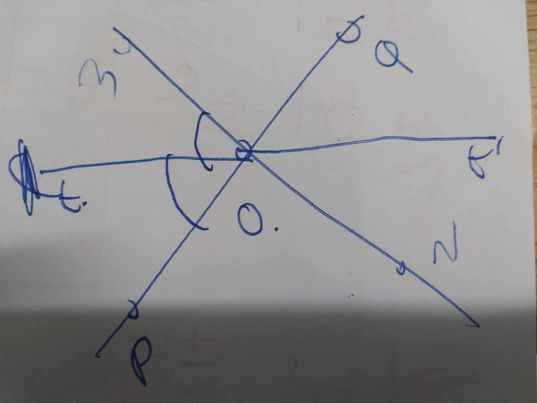
Ot là phân giác của \(\widehat{MOP}\)
=>\(\widehat{MOP}=2\cdot\widehat{tOP}\)
\(\widehat{MOP}=\widehat{NOQ}\)
=>\(\widehat{NOQ}=2\cdot\widehat{tOP}\)
mà \(\widehat{tOP}=\widehat{t'OQ}\)(hai góc đối đỉnh)
nên \(\widehat{NOQ}=2\cdot\widehat{t'OQ}\)
=>Ot' là phân giác của góc NOQ
11:
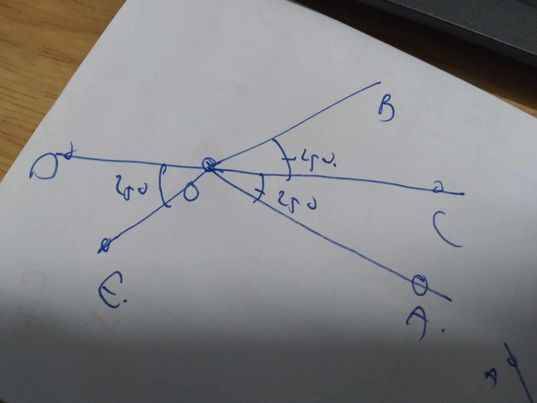
OC là phân giác của góc AOB
=>\(\widehat{AOC}=\widehat{BOC}=\dfrac{50^0}{2}=25^0\)
\(\widehat{DOE}=\widehat{BOC}\left(=25^0\right)\)
=>\(\widehat{DOE}+\widehat{DOB}=180^0\)
=>OB và OE là hai tia đối nhau
=>Hai góc đối đỉnh là \(\widehat{BOC};\widehat{DOE}\)
=>Chọn D
12:
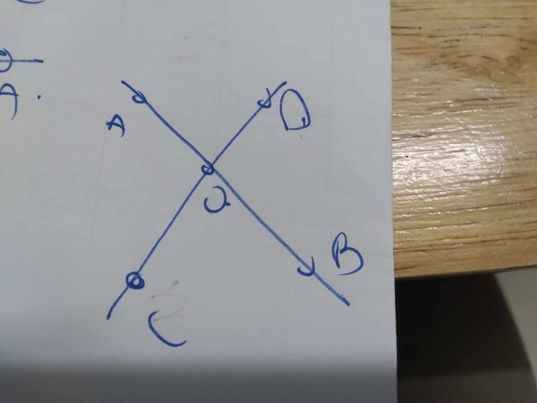
\(\widehat{AOC}+\widehat{AOD}=180^0\)
\(\widehat{AOC}-\widehat{AOD}=50^0\)
Do đó: \(\widehat{AOC}=\dfrac{180^0+50^0}{2}=115^0;\widehat{AOD}=115^0-50^0=65^0\)
=>\(\widehat{BOC}=\widehat{AOD}=65^0\)
=>Chọn B
TT
2
19 tháng 4 2023
a: Xet ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
góc ABD=góc MBD
=>ΔBAD=ΔBMD
b: AD=DM
DM<DC
=>AD<CD
c: Xét ΔDAK vuông tại A và ΔDMC vuông tại M có
DA=DM
góc ADK=góc MDC
=>ΔDAK=ΔDMC
=>AK=MC: DK=DC
=>ΔDKC cân tại D; BK=BC
=>ΔBKC can tại B
mà BN là phân giác
nên BN vuông góc KC
PL
1
6 tháng 7 2023
1.4:
a: CH=16^2/24=256/24=32/3
BC=24+32/3=104/3
AC=căn 32/3*104/3=16/3*căn 13
b: BC=12^2/6=24
AC=căn 24^2-12^2=12*căn 3
CH=24-6=18
MP
1
2 tháng 4 2022
Chiết suất tuyệt đối của kim cương:
Áp dụng công thức: \(n=\dfrac{c}{v}\)
\(\Rightarrow\)Tôc độ truyền ánh sáng trong kim cương:
\(v=\dfrac{c}{n}=\dfrac{3\cdot10^8}{2,42}=1,24\cdot10^8\)m/s=124000km/h
Chọn B.
MC
1
29 tháng 3 2022
Câu 12.
Ta có: \(\dfrac{sini}{sinr}=n\Rightarrow\dfrac{sin60^o}{sinr}=1,5\)
\(\Rightarrow sinr=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow r\approx35,3^o\)
Chọn C
TP
2
MP
1
1 tháng 4 2022
Câu 17.
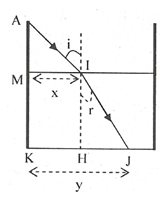
Xét tam giác IHJ vuông tại H:
\(sinr=\dfrac{HJ}{IJ}=\dfrac{HJ}{\sqrt{HI^2+HJ^2}}\)
Chiết xuất: \(\dfrac{sini}{sinr}=n\)
\(\Rightarrow\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{HI^2+HJ^2}}{HJ}=\dfrac{4}{3}\)
\(\Rightarrow\dfrac{3}{4}\cdot\dfrac{60^2+HJ^2}{HJ^2}=\dfrac{16}{9}\Rightarrow HJ=51,25cm\)
Độ dài bóng của thành bể tạo ở đáy:
\(HJ+x=85,9cm\)
Chọn A
MP
1
29 tháng 3 2022
Góc giới hạn phản xạ toàn phần:
\(sini_{gh}=\dfrac{n_2}{n_1}\)
\(\Rightarrow sini_{gh}=\dfrac{\dfrac{4}{3}}{\sqrt{3}}=\dfrac{4\sqrt{3}}{9}\)
\(\Rightarrow i_{gh}=50,2^o\)
Chọn A
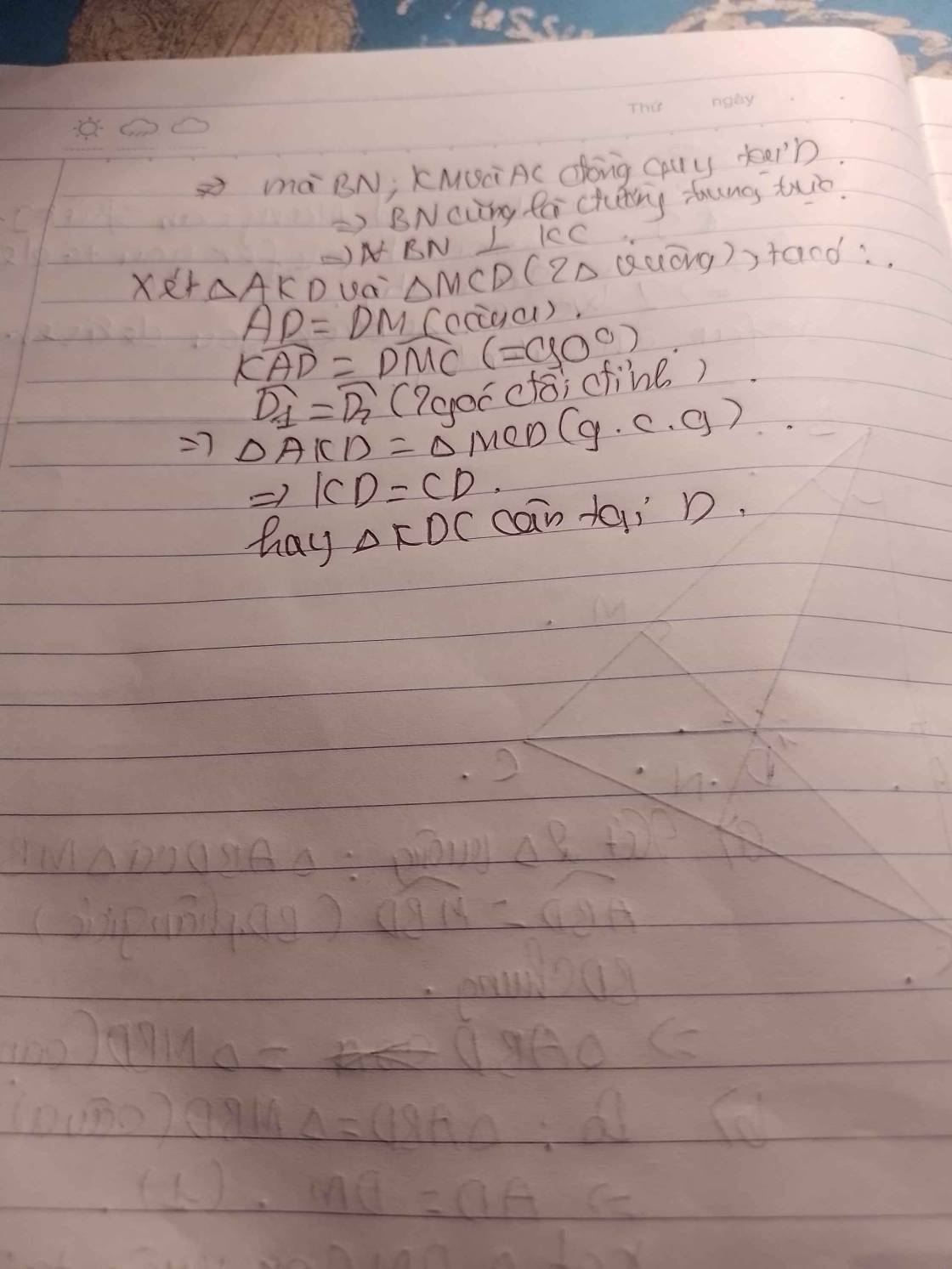
\(1,\)
giải giúp e đc hok ạ