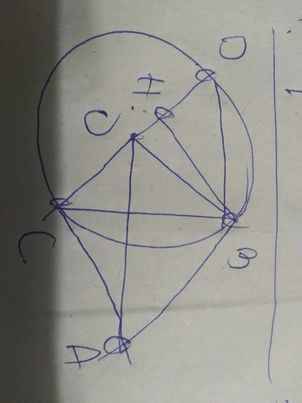
cho 2 đường tròn o bán kính R và đường tròn o' bán kính R' cắt tại 2 điểm A và B.dựng CD là tiếp tuyến chung của 2 đường tròn sao cho B gần CD hơn A. CMR SABC=SABD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 5 2017
Gọi (C) là đường tròn tâm O bán kính r, \(\left(C_1\right)\) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng qua tâm A. Gọi (C') là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C') và \(\left(C_1\right)\).
Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C') và \(\left(C_1\right)\).
6 tháng 1 2023
a: Xét ΔOBA vuông tại B có BH là đường cao
nên OH*OA=OB^2=R^2
b: Xét ΔABC và ΔADB có
góc ABC=góc ADB
góc BAC chung
Do đó; ΔABCđồng dạng với ΔADB
=>AB/AD=AC/AB
=>AB^2=AD*AC
=>AD*AC=AH*AO
28 tháng 12 2023
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại trung điểm K của BC
K là trung điểm của BC
nên \(KB=KC=\dfrac{BC}{2}=12\left(cm\right)\)
Ta có: ΔBKO vuông tại K
=>\(KB^2+KO^2=OB^2\)
=>\(OK^2=15^2-12^2=81\)
=>\(OK=\sqrt{81}=9\left(cm\right)\)
Xét ΔOBA vuông tại B có BK là đường cao
nên \(OK\cdot OA=OB^2\)
=>\(OA=\dfrac{15^2}{9}=25\left(cm\right)\)
Ta có: ΔOBA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=25^2-15^2=400\)
=>\(BA=\sqrt{400}=20\left(cm\right)\)
c: Sửa đề: E là giao điểm của AC và BD
Ta có: BH\(\perp\)CD
AC\(\perp\)CD
Do đó: BH//CD
Xét ΔDCA có HI//CA
nên \(\dfrac{HI}{CA}=\dfrac{DI}{DA}\left(3\right)\)
Xét ΔDAE có IB//AE
nên \(\dfrac{IB}{AE}=\dfrac{DI}{DA}\left(4\right)\)
Xét (O) có
ΔDBC nội tiếp
DC là đường kính
Do đó: ΔDBC vuông tại B
=>DB\(\perp\)BC tại B
=>BC\(\perp\)DE tại B
=>ΔCBE vuông tại B
Ta có: \(\widehat{ABE}+\widehat{ABC}=\widehat{CBE}=90^0\)
\(\widehat{AEB}+\widehat{ACB}=90^0\)(ΔCBE vuông tại B)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABE}=\widehat{AEB}\)
=>AB=AE
mà AB=AC
nên AE=AC
Từ (3) và (4) suy ra \(\dfrac{HI}{CA}=\dfrac{IB}{AE}\)
mà CA=AE
nên HI=IB
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2020
\(ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\left\{{}\begin{matrix}\widehat{ACB}+\widehat{BCH}=90^0\\\widehat{CBH}+\widehat{BCH}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{ACB}=\widehat{CBH}\)
\(\Rightarrow\widehat{ABC}=\widehat{CBH}\)
17 tháng 11 2023
a: Xét (O) có
CM,CA là tiếp tuyến
Do đó: CM=CA và OC là phân giác của \(\widehat{AOM}\)
=>\(\widehat{COM}=\dfrac{1}{2}\cdot\widehat{MOA}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của \(\widehat{MOB}\)
=>\(\widehat{MOD}=\dfrac{1}{2}\cdot\widehat{MOB}\)
\(\widehat{COD}=\widehat{COM}+\widehat{DOM}\)
\(=\dfrac{1}{2}\cdot\widehat{MOA}+\dfrac{1}{2}\cdot\widehat{MOB}\)
\(=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
CD=CM+MD
mà CM=CA và DM=DB
nên CD=CA+DB
b: Xét ΔOCD vuông tại O có OM là đường cao
nên \(OM^2=CM\cdot MD\)
=>\(AC\cdot BD=R^2\)
c: CM=CA
OM=OA
Do đó: CO là đường trung trực của AM
=>CO\(\perp\)AM tại E
DM=DB
OM=OB
Do đó: OD là đường trung trực của MB
=>OD\(\perp\)MB tại F
Xét tứ giác MEOF có
\(\widehat{MEO}=\widehat{MFO}=\widehat{FOE}=90^0\)
=>MEOF là hình chữ nhật
=>EF=OM=R