Tìm giá trị của x để \(M=\dfrac{x^3-25x}{x^2+10x+25}\) có giá trị bằng 0.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) x ≠ -5.
b) Ta có P = ( x + 5 ) 2 x + 5 = x + 5
c) Ta có P = 1 Û x = -4 (TMĐK)
d) Ta có P = 0 Û x = -5 (loại). Do vậy x ∈ ∅ .

Biểu thức x 2 - 25 x 2 - 10 x + 25 x xác định khi x 0 và x ≠ 5.
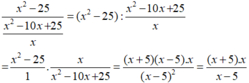
Ta có: 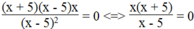 khi x(x + 5) = 0 và x – 5
≠
0
khi x(x + 5) = 0 và x – 5
≠
0
x(x + 5) = 0 ⇔ x = 0 hoặc x + 5 = 0 ⇔ x = - 5
x = 0 không thỏa mãn điều kiện.
Vậy x = - 5 thì biểu thức x 2 - 25 x 2 - 10 x + 25 x có giá trị bằng 0.

a)
2x-3=0 => x=3/2
b)
2x^2 +1 =0 => vô nghiệm
c) x^2 -25 =0 => x=5 loiaj
x=-5 nhân
d)
x^2 -25 =0 => x=5 loại
x=-5 loại

Biểu thức x 2 - 25 x 2 + 10 x + 25 x - 5 xác định khi x ≠ 5 và x ≠ - 5
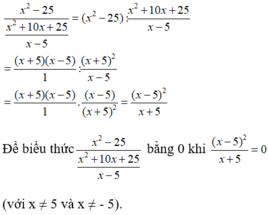
x - 5 2 = 0 ⇔ x – 5 = 0 ⇔ x= 5
x = 5 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để biểu thức x 2 - 25 x 2 + 10 x + 25 x - 5 có giá trị bằng 0.

Phân thức 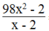 = 0 khi
98
x
2
+
2
=
0
và x – 2
≠
0
= 0 khi
98
x
2
+
2
=
0
và x – 2
≠
0
Ta có: x – 2 ≠ 0 ⇔ x ≠ 2
98 x 2 + 2 = 0 ⇔ 2 49 x 2 - 1 = 0 ⇔ (7x + 1)(7x – 1) = 0
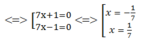
Ta có: 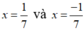 thỏa mãn điều kiện x
≠
2
thỏa mãn điều kiện x
≠
2
Vậy ![]() thì phân thức
thì phân thức ![]() có giá trị bằng 0.
có giá trị bằng 0.

Phân thức 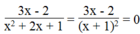 khi 3x – 2 = 0 và
x
+
1
2
≠
0
khi 3x – 2 = 0 và
x
+
1
2
≠
0
Ta có: x + 1 2 ≠ 0 ⇔ x + 1 ≠ 0 ⇔ x ≠ - 1
3x – 2 = 0 ⇔ 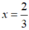
Ta có: 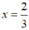 thỏa mãn điều kiện x
≠
- 1
thỏa mãn điều kiện x
≠
- 1
Vậy 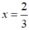 thì phân thức
thì phân thức 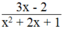 có giá trị bằng 0.
có giá trị bằng 0.


Điều kiện cuả biến:
x2−5x=x(x−5)≠0;x−5≠0x2−5x=x(x−5)≠0;x−5≠0 hay x≠0;x≠5x≠0;x≠5
Do đó điều kiện của biến là x≠0;x≠5x≠0;x≠5
Rút gọn phân thức:
x2−10x+25x2−5x=(x−5)2x(x−5)=x−5xx2−10x+25x2−5x=(x−5)2x(x−5)=x−5x
Phân thức có giá trị bằng 0 khi x−5x=0x−5x=0
Hay x−5=0vàx≠0x−5=0vàx≠0 hay x = 5
Nhưng x = 5 không thỏa mãn điều kiện của biến. Vậy không có giá trị nào của x để giá trị của phân thức thức 0.
ĐKXĐ : \(x^2+10x+25\ne0\Leftrightarrow\left(x+5\right)^2\ne0\Leftrightarrow x\ne-5\)
Để \(M=0\)
\(\Leftrightarrow\dfrac{x^3-25x}{x^2+10x+25}=0\)
\(\Leftrightarrow x^3-25x=0\)
\(\Leftrightarrow x\left(x^2-25\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-25=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\\left(x-5\right)\left(x+5\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\) ( đối chiếu theo đkxđ : \(x\ne-5\) )
Vậy ...
ĐKXĐ:
\(x^2+10x+25\ne0\Leftrightarrow\left(x+5\right)^2\ne0\Leftrightarrow x\ne-5\)
\(M=\dfrac{x^3-25x}{\left(x+5\right)^2}=\dfrac{x\left(x^2-25\right)}{\left(x+5\right)^2}=\dfrac{x\left(x+5\right)\left(x-5\right)}{\left(x+5\right)^2}=\dfrac{x\left(x-5\right)}{x+5}\)
\(\Rightarrow M=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(thoa\right)\\x=5\left(thoa\right)\end{matrix}\right.\)
Vậy x = 0 hoặc x = 5