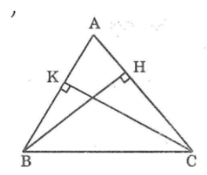
Cho tam giác ABC nhọn. Qua B kẻ BH vuông góc AC ( H thuộc AC ); qua C kẻ CK vuông góc AB ( K thuộc AB ). Trên tia đối của tia BH lấy điểm M sao cho BM = AC, trên tia đối của tia CK lấy điểm N sao cho CN = AB. Chứng minh:
a) Góc ABH = góc ACK
b) Tam giác ABM = tam giác NCA
c) AM vuông góc với AN