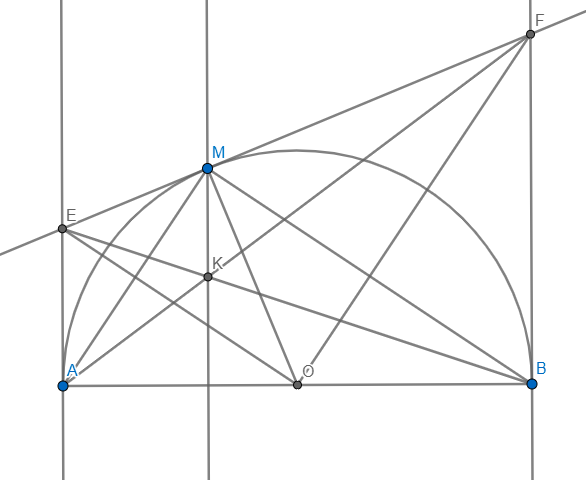
Cho nửa dg tròn (O) dg kính AB . Gọi Ax,By là các tia vuông goc với AB ( Ax,By và nửa dg tròn cùng thuộc mọt nửa mặt phẳng bờ AB) . Qua điểm M thuôc nửa dg tròn ( M khác A ,B ) ke tiếp tuyến với nửa dg tròn , nó cát Ax tại C và cắt By tai D.
a) Cm : CD = AC+BD và Góc COD = 90°
b) AD cắt BC tại N . CM :MN\\ BD
c) tích AC.BD ko đổi khi điểm M di chuyển tren nưa dg tron
d) gọi H là trung diểm cua AM . Cm: ba điểm O,H,C thẳng hàng

a: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
CD=CM+MD
=>CD=CA+BD
c: AC*BD=MC*MD=OM^2=R^2 ko đổi
d: CM=CA
OM=OA
Do đó: CO là trung trực của AM
mà H nằm trên đường trung trực của AM
nên O,H,C thẳng hàng