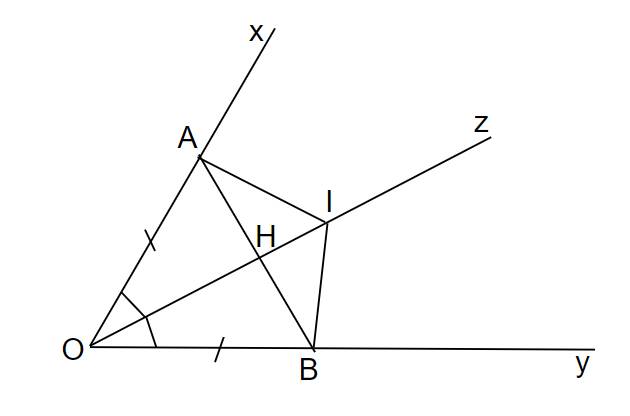
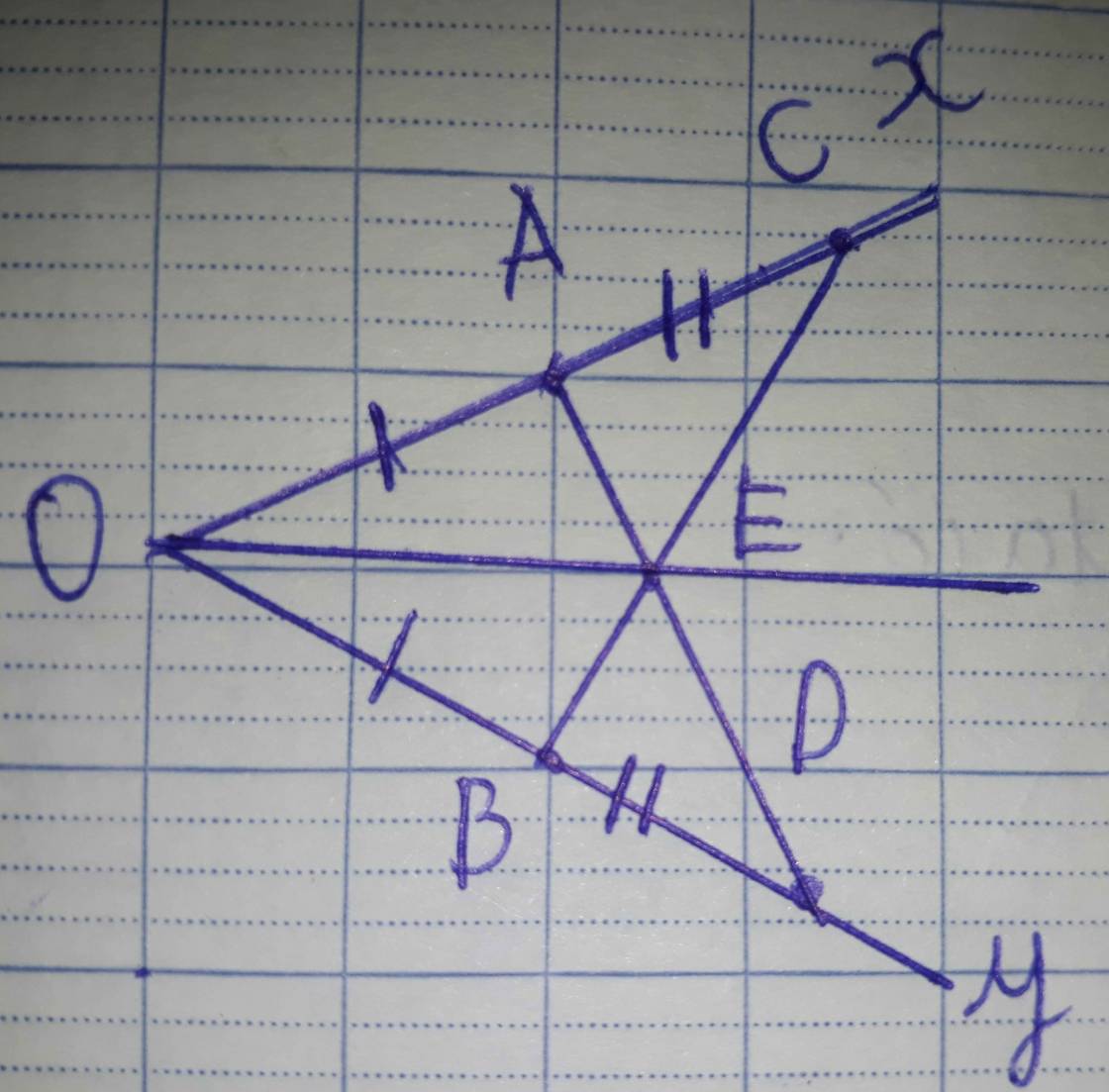
Cho góc nhọn xOy. Trên tia Ox lấy 2 điểm A,B (OA<OB). Trên tia Oy lấy 2 điểm C,D sao cho OC=OA; OD=OB. Gọi I là giao điểm của AD và BC:
1. Chứng minh tam giác OAD bằng tam giác OCB.
2. Chứng minh OI là tia phân giác của góc xOy.
3. Chứng minh AC song song với BD.