biết xy+yz+xz=3 và xyz=1a, rút gọn biểu thức sau:A= x+y+z/zy2+xz2+xy2b, nếu x.y2.z3=64 tính Agiúp...
Đọc tiếp
biết xy+yz+xz=3 và xyz=1
a, rút gọn biểu thức sau:
A= x+y+z/zy2+xz2+xy2
b, nếu x.y2.z3=64 tính A
giúp nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
0
2 tháng 7 2021
b, đk: \(x\ge1,y\ge2,z\ge3\)
\(=>B=\dfrac{\sqrt{x-1}}{x}+\dfrac{\sqrt{y-2}}{y}+\dfrac{\sqrt{z-3}}{z}\)
đặt \(\left\{{}\begin{matrix}\sqrt{x-1}=a\\\sqrt{y-2}=b\\\sqrt{z-3}=c\end{matrix}\right.\)\(=>\left\{{}\begin{matrix}x=a^2+1\\y=b^2+1\\z=c^2+1\end{matrix}\right.\)\(=>a\ge0,b\ge0,c\ge0\)
B trở thành \(\dfrac{a}{a^2+1}+\dfrac{b}{b^2+1}+\dfrac{c}{c^2+1}\)
\(=\dfrac{a^{ }}{a^2+1}+\dfrac{a^2+1}{4}+\dfrac{b}{b^2+1}+\dfrac{b^2+1}{4}+\dfrac{c}{c^2+1}+\dfrac{c^2+1}{4}\)
\(-\left(\dfrac{a^2+b^2+c^2+3}{4}\right)\ge\sqrt{a}+\sqrt{b}+\sqrt{c}-\dfrac{a^2+b^2+c^2}{4}\)\(=0\)
dấu"=" xảy ra<=>\(a=0,b=0,c=0< =>x=1,y=2,z=3\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 7 2021
Chắc bạn ghi nhầm đề, tìm GTLN mới đúng, chứ GTNN của các biểu thức này đều hiển nhiên bằng 0
\(A=\dfrac{3.\sqrt{x-9}}{15x}\le\dfrac{3^2+x-9}{30x}=\dfrac{1}{30}\)
\(A_{max}=\dfrac{1}{30}\) khi \(x=18\)
\(B=\dfrac{\sqrt{x-1}}{x}+\dfrac{\sqrt{y-2}}{y}+\dfrac{\sqrt{z-3}}{z}=\dfrac{1.\sqrt{x-1}}{x}+\dfrac{\sqrt{2}.\sqrt{y-2}}{\sqrt{2}y}+\dfrac{\sqrt{3}.\sqrt{z-3}}{\sqrt{3}z}\)
\(B\le\dfrac{1+x-1}{2x}+\dfrac{2+y-2}{2\sqrt{2}y}+\dfrac{3+z-3}{2\sqrt{3}z}=\dfrac{1}{2}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}\)
Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(2;4;6\right)\)
TN
2
2 tháng 1 2018
\(M=\frac{x}{xy+x+2015}+\frac{y}{yz+y+1}+\frac{2015z}{xz+2015z+2015}\)
\(\Leftrightarrow M=\frac{x}{xy+x+xyz}+\frac{y}{yz+y+1}+\frac{xyz.z}{xz+xyz.z+xyz}\left(xyz=2015\right)\)
\(\Leftrightarrow M=\frac{1}{y+1+yz}+\frac{y}{yz+y+1}+\frac{yz}{1+yz+y}\)
\(\Leftrightarrow M=\frac{yz+y+1}{yz+y+1}=1\)
2 tháng 1 2018
\(M=\frac{x}{xy+x+2015}+\frac{y}{yz+y+1}+\frac{2015z}{xz+2015z+2015}\)
Thay xyz = 2015, Ta có:
\(M=\frac{x}{xy+x+xyz}+\frac{y}{yz+y+1}+\frac{xyz^2}{xz+xyz^2+xyz}\)
\(M=\frac{1}{y+1+yz}+\frac{y}{yz+y+1}+\frac{yz}{1+yz+y}\)
\(M=\frac{y+1+yz}{y+1+yz}=1\)
PT
1
CM
22 tháng 4 2019
M = x 3 + y 3 + z 3 - 3 x y z x 2 + y 2 + z 2 - x y - y z - x z
K
11 tháng 9 2021
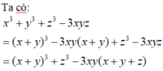
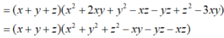
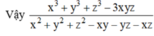
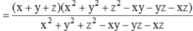
Ta có \(\frac{x+2xy+1}{x+xy+xz+1}=\frac{x+2xy+xyz}{x+xy+xz+xyz}=\frac{1+2y+yz}{\left(y+1\right)\left(z+1\right)}\)
Tương tự => \(M=\frac{1+2y+yz}{\left(y+1\right)\left(z+1\right)}+\frac{1+2z+zx}{\left(1+x\right)\left(z+1\right)}+\frac{1+2x+xy}{\left(1+x\right)\left(y+1\right)}\)
=> \(M=\frac{\left(1+2y+yz\right)\left(1+x\right)+\left(1+2z+zx\right)\left(1+y\right)+\left(1+2x+xy\right)\left(1+z\right)}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\)
=>\(M=\frac{6+3\left(x+y+z\right)+3\left(xy+yz+xz\right)}{2+\left(x+y+z\right)+\left(xy+yz+xz\right)}=3\)
HY
0
20 tháng 2 2017
\(\frac{xy+2x+1}{xy+x+y+1}+\frac{yz+2y+1}{yz+y+z+1}+\frac{zx+2z+1}{zx+z+x+1}\)
Ta có: \(\frac{xy+2x+1}{xy+x+y+1}=\frac{\left(xy+x\right)+\left(x+1\right)}{\left(xy+x\right)+\left(y+1\right)}=\frac{x\left(y+1\right)+\left(x+1\right)}{\left(y+1\right)\left(x+1\right)}=\frac{x}{x+1}+\frac{1}{y+1}\)
Tương tự ta có:
\(\frac{yz+2y+1}{yz+y+z+1}=\frac{y}{y+1}+\frac{1}{z+1}\)
\(\frac{zx+2z+1}{zx+z+x+1}=\frac{z}{z+1}+\frac{1}{x+1}\)
Từ đây ta có biểu thức ban đầu sẽ bằng
\(\frac{x}{x+1}+\frac{1}{y+1}+\frac{y}{y+1}+\frac{1}{z+1}+\frac{z}{z+1}+\frac{1}{x+1}\)
\(\left(\frac{x}{x+1}+\frac{1}{x+1}\right)+\left(\frac{y}{y+1}+\frac{1}{y+1}\right)+\left(\frac{z}{z+1}+\frac{1}{z+1}\right)=1+1+1=3\)
20 tháng 2 2017
CHÚ Ý: ab+a+b+1=a(b+1)+(b+1)=(a+1)(b+1)
Xét: \(\frac{xy+2x+1}{xy+x+y+1}=\frac{x\left(y+1\right)+x+1}{\left(x+1\right)\left(y+1\right)}=\frac{x}{x+1}+\frac{1}{y+1}\)
Tương tự với 2 biểu thức còn lại ta được:
A=\(\frac{x}{x+1}+\frac{1}{y+1}+\frac{y}{y+1}+\frac{1}{z+1}+\frac{z}{z+1}+\frac{1}{x+1}\)
=\(\frac{x+1}{x+1}+\frac{y+1}{y+1}+\frac{z+1}{z+1}=1+1+1=3\)