tính số đo của mỗi góc ngoài của một lục giác đều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Cho 1 hình lục giác đều ta kẻ 3 đường thẳng như hình vẽ trên, thu được 4 tam giác.
Tổng số đo các góc của 1 tam giác bằng 180o.
Mà hình trên có 4 tam giác.
⇒⇒ Tổng các góc của 4 tam giác đó là 180o.4=720o180o.4=720o
Vậy tổng các góc của 1 lục giác đều là 720o
Cho 1 hình lục giác đều ta kẻ 3 đường thẳng như hình vẽ trên, thu được 4 tam giác.
Tổng số đo các góc của 1 tam giác bằng 180o.
Mà hình trên có 4 tam giác.
⇒ Tổng các góc của 4 tam giác đó là 180o.4=720o
Vậy tổng các góc của 1 lục giác đều là 720o
\(\text{Chúc bạn học tốt }(\text{Nhớ kick mình nhé}:3)\)


Cho 1 hình lục giác đều ta kẻ 3 đường thẳng như hình vẽ trên, thu được 4 tam giác.
Tổng số đo các góc của 1 tam giác bằng 180o.
Mà hình trên có 4 tam giác.
⇒⇒ Tổng các góc của 4 tam giác đó là 180o.4=720o180o.4=720o
Vậy tổng các góc của 1 lục giác đều là 720o
Chúng ta đã biết tổng số đo tất cả các góc ngoài của một đa giác đều bất kỳ đều bằng 360 độ và các góc ngoài đều bằng nhau
=> Số đo mỗi góc ngoài của lục giác đều là: 360/6=60 độ

a) Tổng số đo các góc của một đa giác n cạnh = \((7-2).180^0\) = \(900^0\)
b)Số đo mỗi góc của ngũ giác đều là : \(\frac{(5-2).180^0}{5}\)= \(108^0\)
Số đo mỗi góc của lục giác đều là \(\frac{(6-2).180^0}{6}\)= \(120^0\)


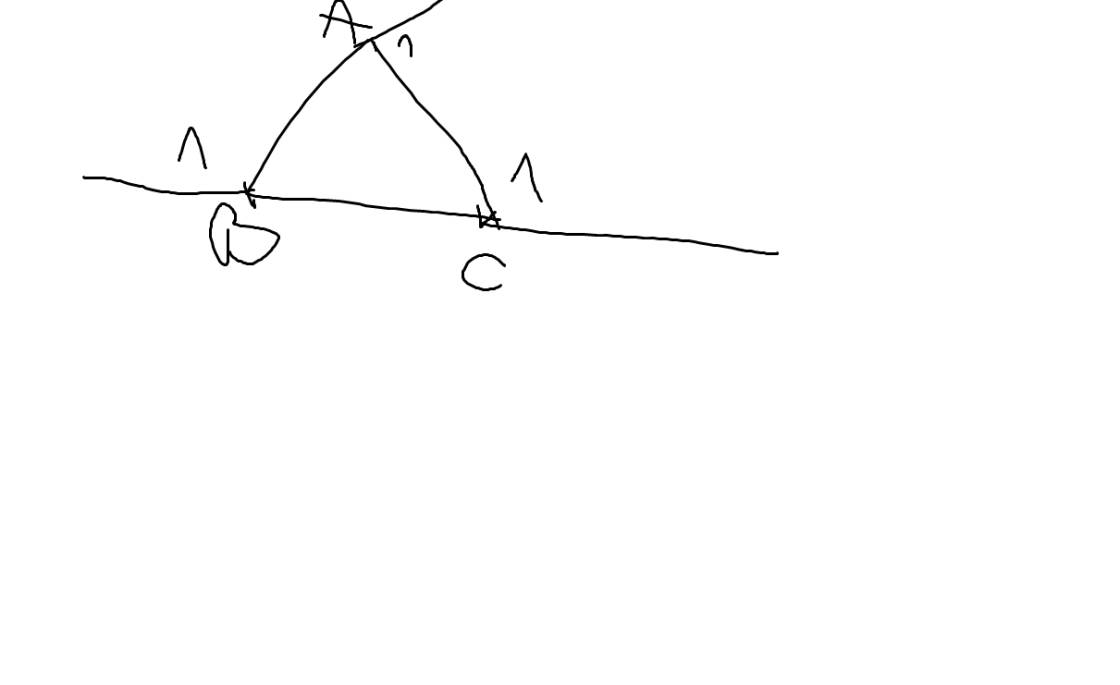
Gọi \(\widehat{A_1};\widehat{B_1};\widehat{C_1}\) lần lượt là các góc ngoài tại các đỉnh A,B,C của ΔABC
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\widehat{B_1}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{B_1}=180^0-\widehat{ABC}\)
\(\widehat{C_1}+\widehat{ACB}=180^0\)(hai góc kề bù)
=>\(\widehat{C_1}=180^0-\widehat{ACB}\)
\(\widehat{A_1}+\widehat{BAC}=180^0\)(hai góc kề bù)
=>\(\widehat{A_1}=180^0-\widehat{BAC}\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}\)
\(=180^0-\widehat{BAC}+180^0-\widehat{ABC}+180^0-\widehat{ACB}\)
\(=540^0-180^0=360^0\)


