Cho tam giác ABC có 3 góc nhọn và M là điểm nằm trên BC. Gọi E,F lần lượt là hình chiếu của B và C xuống AM. Xác định vị trí của M trên BC để tổng BE+CF lớn nhất
Gợi ý: BE+CF< HOẶC = BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
10 tháng 9 2019
Mình nói trước là mình mới học dạng này nên không chắc đâu nhé! Nhất là cái dấu "=" ấy, nó rất khó để giải thích và có thể sai. Nếu bạn dùng geogebra thì sẽ dễ hiểu hơn.
Đặt BC = a = const (hằng số)
Xét trường hợp E và F không trùng D. Khi đó theo quan hệ giữa đường vuông góc và đường xiên thì:
BE + CF < BD + CD = BC (1)
Nếu E và F trùng D thì BE + CF = BC (2)
Từ (1) và (2) suy ra \(BE+CF\le BC=const\)
Đẳng thức xảy ra khi E và F trùng D khi đó D là trung điểm BC và tam giác ABC cân tại A.
11 tháng 9 2019
tth làm không đúng rồi.
Ta có E là hình chiếu của B lên AD
F là hình chiếu của CAD
=> \(BC=BD+DC\ge BE+CF\)
Dấu "=" xảy ra khi và chỉ khi \(E\equiv D\equiv F\)
khi đó: \(BD\perp AD;CD\perp AD\)=> D là chân đường cao hạ từ A đến BC
Vậy D là chân đường cao hạ từ A đến BC thì BE+CF đạt giá trị lớn nhất bằng BC
KN
24 tháng 1 2020
Theo giả thiết ta có: \(CF\perp AM\)nên \(\Delta MCF\)vuông tại F
Suy ra CF < MC (cạnh góc vuông bé hơn cạnh huyền) (1)
Tương tự ta có: BE < BM (2)
Từ (1) và (2) suy ra \(BE+CF< BM+MC=BC\)
Vậy \(BE+CF< BC\left(đpcm\right)\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
18 tháng 3 2021
a/
Ta thấy F và E đều nhìn BC dưới cùng 1 góc 90 độ nên E,F nằm trên đường tròn đường kính BC ta gọi là đường tròn (O')
=> B,F,E,C cùng nawmg trên một đường tròn
b/
Xét đường tròn (O) ta có
sđ \(\widehat{BQP}=\) sđ \(\widehat{BCP}=\frac{1}{2}\) sđ cung BP (góc nội tiếp đường tròn) (1)
Xét đường tròn (O') ta có
sđ \(\widehat{BEF}=\) sđ \(\widehat{BCP}=\frac{1}{2}\) sđ cung BF (góc nội tiếp đường tròn) (2)
Từ (1) và (2) \(\Rightarrow\widehat{BQP}=\widehat{BEF}\) => PQ//EF (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 có hai góc ở vị trí đồng vị thì chúng // với nhau
c/ ta thấy F và D cùng nhìn BH dưới cùng 1 góc 90 độ nên BDHF là tứ giác nội tiếp
sđ \(\widehat{ABE}=\)sđ \(\widehat{FDA}=\frac{1}{2}\) sđ cung FH (1)
Ta thấy D và E cùng nhìn AB đướ cùng 1 góc 90 độ nên ABDE là tứ giác nội tiếp
sđ \(\widehat{ABE}=\)sđ \(\widehat{ADE}=\frac{1}{2}\) sđ cung AE (2)
Mà \(\widehat{FDA}+\widehat{ADE}=\widehat{FDE}\) (3)
Từ (1) (2) và (3) \(\Rightarrow\widehat{FDE}=2.\widehat{ABE}\left(dpcm\right)\)
NN
23 tháng 4 2019
bạn ơi cho mình hỏi bài này ở đề năm bao nhiêu của thành phố nào vậy bạn?????
VT
2 tháng 5 2019
3. Xét tứ giác BFHD có:
HFB + HDB = 90º + 90º = 180º => BFHD là tứ giác nội tiếp. ⇒ FBH = FDH (1)
Tương tự có DHEC là tứ giác nội tiếp, ⇒HCE = HDE (2)
Mà BFEC là tứ giác nội tiếp nên FCE = FBE (3)
Từ (1) (2) (3)⇒ 2ABE = FDH + HDE = FDE
Vì BFEC là tứ giác nội tiếp đường tròn tâm I, đường kính BC nên theo quan hệ giữa góc ở tâm và góc nội tiếp cùng chắn cung EF, ta có: FIE = 2.FBE = 2.ABE
⇒FIE = FDE
4.Vì BFEC là tứ giác nội tiếp nên:
ABC = 180º – FEC = AEF => ΔAEF ~ ΔABC (g.g)
Suy ra độ dài EF không đổi khi A chạy trên cung lớn BC của đường tròn (O)
Gọi K là giao điểm thứ 2 của ED và đường tròn đường kính BC
Theo tính chất góc ngoài: FDE = DKE + DEK
Theo ý 3 và quan hệ giữa góc ở tâm và góc nội tiếp cùng chắn cung, có FDE = FIE = 2.DKE
⇒DKE = DEK => ΔDEK cân tại D => DE = DK
Chu vi ΔDEF là P = DE + EF + FD = EF + FD + DK = EF + FK
Có FK ≤ BC ( dây cung – đường kính) => P ≤ EF + BC không đổi
Dâu bằng xảy ra khi và chỉ khi FK đi qua I ⇔ D trùng I ⇔ ΔABC cân tại A.
Vậy A là điểm chính giữa của cung lớn BC
CM
12 tháng 10 2019
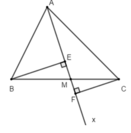
Vì BE ⊥ Ax tại E nên tam giác BEM vuông tại E ⇒ BM > BE (quan hệ đường xiên và đường vuông góc)
Vì CF ⊥ Ax tại F nên tam giác CFM vuông tại F ⇒ CM > CF (quan hệ đường xiên và đường vuông góc)
Khi đó ta có: BM + CM > BE + CF
Mà BM + CM = BC (M thuộc BC)
Do đó: BC > BE + CF hay BE + CF < BC.
Chọn đáp án A