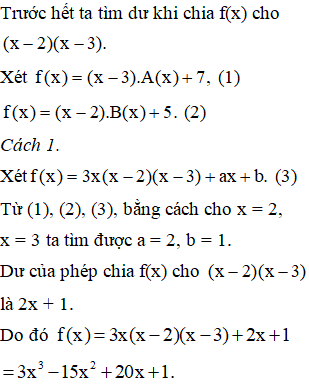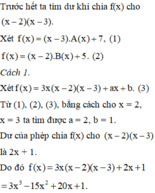Tim f(x) biêt f(x):(x-2) dư 5;f(x):(x-3) dư 7 ;f(x):(x-2)(x-3) đươc thương 3x còn dư
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
1 tháng 7 2023
Lời giải:
Gọi $ax+b$ là dư của $F(x)$ khi chia cho $(x+2)(x-5)$
Ta có:
$F(x)=2x(x+2)(x-5)+ax+b(*)$
Theo đề thì $F(-2)=8; F(5)=26$
Thay $x=-2$ vào $(*)$ thì:
$F(-2)=(-2)a+b=8(1)$
$F(5)=5a+b=26(2)$
Từ $(1); (2)\Rightarrow a=\frac{18}{7}; b=\frac{92}{7}$
Khi đó:
$F(x)=2x(x+2)(x-5)+\frac{18}{7}x+\frac{92}{7}$
$=2x^3-6x^2-\frac{122x}{7}+\frac{92}{7}$
6 tháng 7 2018
GỌI THƯƠNG CỦA PHÉP CHIA f(x) cho (x-2) và (x+5) lần lượt là p(x) và Q(x)
theo bài ra ta có
\(\hept{\begin{cases}f._x=\left(x-2\right).p._{\left(x\right)}+1............\left(1\right)\\f._{\left(x\right)}=\left(x+5\right).Q._{\left(x\right)}+8.......\left(2\right)\end{cases}}\)
GỌI THƯƠNG CỦA PHÉP CHIA f(x) cho (x-2)(x+5) [ là x^2+3x-10 phân tích thành] =2x là g(x) và số dư là nhị thức bậc nhất là ax+b
ta có, \(f._{\left(x\right)}=\left(x-2\right)\left(x+5\right).g._{\left(x\right)}+ax+b....................\left(3\right)\)
TỪ (1) VÀ (3) TA CÓ X=2 THÌ \(\hept{\begin{cases}f._2=1\\f_2=2a+b\end{cases}}\)
=> 2a+b=1 =>b=1-2a (4)
TỪ (2) VÀ (3) TA CÓ X=-5 THÌ \(\hept{\begin{cases}f_{\left(-5\right)}=8\\f_{\left(-5\right)}=-5a+b\end{cases}}\)
=> 8=-5a+b =>b=8+5a (5)
TỪ (4) VÀ (5) =>1-2a=8+5a <=> a=-1
=> b=3
vậy số dư là -x+3
vậy đa thức f(x) =(x-2)(x+5) .2x+(-x+3)=\(2x^3+6x^2-21x+3\)
LT
2
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2019
\(x=1\Rightarrow3f\left(4\right)=0\Rightarrow f\left(4\right)=0\Rightarrow x=4\) là nghiệm
\(x=-2\Rightarrow-3.f\left(-2\right)=0\Rightarrow f\left(-2\right)=0\Rightarrow x=-2\) là nghiệm
Tới đây thì xử lý như sau:
Để ý 2 vế ta có \(x-\left(x-1\right)=\left(x+3\right)-\left(x+2\right)=1\) nên 2 vế cùng dạng
Mà \(x+3\) hơn \(x\) đúng 3 đơn vị, nên ta chỉ việc tiến lùi 2 giá trị ở trên 3 đơn vị thì muốn bao nhiêu nghiệm cũng có hết
Ví dụ tiến 3 ta sẽ có các giá trị cần thay vào là 4;7;10;13;16...:
\(x=4\Rightarrow6f\left(7\right)=3f\left(4\right)=3.0=0\Rightarrow f\left(7\right)=0\Rightarrow x=7\) là nghiệm
\(x=7\Rightarrow9f\left(10\right)=6f\left(7\right)=6.0=0\Rightarrow f\left(10\right)=10\Rightarrow x=10\) là nghiệm
\(x=10\Rightarrow12f\left(13\right)=9f\left(10\right)=0\Rightarrow x=13\) là nghiệm
Một tỉ nghiệm cũng dư xài
M
23 tháng 8 2023
Để tìm dư của phép chia đa thức f(x) cho (x^2 + 1)(x - 2), chúng ta cần sử dụng định lý dư của đa thức. Theo định lý dư của đa thức, nếu chia đa thức f(x) cho đa thức g(x) và được dư đa thức r(x), thì ta có: f(x) = q(x) * g(x) + r(x) Trong trường hợp này, chúng ta biết rằng f(x) chia cho x - 2 dư 7 và chia cho x^2 + 1 dư 3x + 5. Vì vậy, chúng ta có các phương trình sau: f(x) = q(x) * (x - 2) + 7 f(x) = p(x) * (x^2 + 1) + (3x + 5) Để tìm dư của phép chia f(x) cho (x^2 + 1)(x - 2), ta cần tìm giá trị của r(x). Để làm điều này, chúng ta cần giải hệ phương trình trên. Đầu tiên, chúng ta sẽ giải phương trình f(x) = q(x) * (x - 2) + 7 để tìm giá trị của q(x). Sau đó, chúng ta sẽ thay giá trị của q(x) vào phương trình f(x) = p(x) * (x^2 + 1) + (3x + 5) để tìm giá trị của p(x) và r(x). Nhưng trước tiên, chúng ta cần biết đa thức f(x) là gì. Bạn có thể cung cấp thông tin về đa thức f(x) không?