cho hình thang ABCD có diện tích 50m vuông. Kéo dài AB 1 đoạn BE=AB, kéo dài BC một đoạn CG=BC, kéo dài CD một đoạn DH=CD, kéo dài AD một đoạn AK=AD. Tính diện tích tứ giác EGHK?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DP
30 tháng 6 2017
Nối E , G , H , K . Ta được :
- \(S_{KAB}=S_{ABD}\) (vì \(AK=AD\)và chung đường cao hạ từ đỉnh \(B\).)
-\(S_{AKE}=S_{KAB}\cdot2\)(vì \(S_{KAB}=S_{KBE}\)chung đường cao hạ từ đỉnh \(K\)và \(AB=BE\))
\(\Rightarrow S_{KAE}=S_{ABD}\cdot2\) và \(S_{GHC}=S_{BCD}\cdot2\)
\(\Rightarrow S_{ABCD}\cdot2=S_{KAE}+S_{GHC}=S_{ABD}\cdot2+S_{BCD}\cdot2\)
\(\Rightarrow S_{EGHK}=30\times5=150\left(m^2\right)\)
ĐS: 150 m2
BT
15 tháng 6 2021
Cho hình thang ABCD có diện tích = 60m2, kéo dài BC 1 đoạn BE= ab, kéo dài BC 1 đoạn CG= BC, kéo dài Cd 1 đoạn Dh = CD. kéo dài DA 1 đoạn AK= AD. Tính diện tchs hình tứ giác ABCD
20 tháng 3 2017
kẻ ac và bd có tâm là o
xét tam giác aek và ado thì đấy = nhau , chiều cao aek gấp đôi chiều cao adb
aek có diện tích gấp đôi adb
tương tự khd gấp đôi bcd
như vậy kae +dhk = 30 x 2 =60 m2
tương tự như vậy thì bge +ghc =60 m2
diện tích tứ giác eghk =60 +60 +30 =150 m2
ds 150 m2
chúc bạn học giỏi
20 tháng 1 2017
chịu lên mạng có giải được đâu khó lắm , nếu biết cách làm nho chi nhe
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
10 tháng 9 2020
Nối M với C; N với D; P với A và Q với B
Nối A với C; B với D
Ta có S(ABCD)=S(ABD)+S(BCD)=S(ABC)+S(ACD)
Xét tg ABQ và tg ABD có chung đường cao hạ từ B xuống DQ và cạnh đáy AQ=AD nên S(ABQ)=S(ABD)
Xét tg ABQ và tg BMQ có chung đường cao hạ từ Q xuống AM và cạnh đáy AB=BM nên S(ABQ)=S(BMQ)
=> S(ABQ)=S(BMQ)=S(ABD) => S(AMQ)=S(ABQ)+S(BMQ)=2xS(ABD) (1)
Chứng minh tương tự khi xét các tam giác BCD với tg CDN và tg CDN với tg DNQ => S(CNP)=2xS(BCD) (2)
Từ (1) và (2) => S(AMQ)+S(CNP)=2xS(ABD)+2xS(BCD)=2x[S(ABD)+S(BCD)]=2xS(ABCD)
Chứng minh tương tự ta sẽ có kết quả S(DPQ)+S(CMN)=2x[S(ACD)+S(ABC)]=2xS(ABCD)
S(MNPQ)=[S(AMQ)+S(CNP)]+[S(DPQ)+S(CMN)]+S(ABCD)=5xS(ABCD)=5x25=125 cm2
3 tháng 4 2023
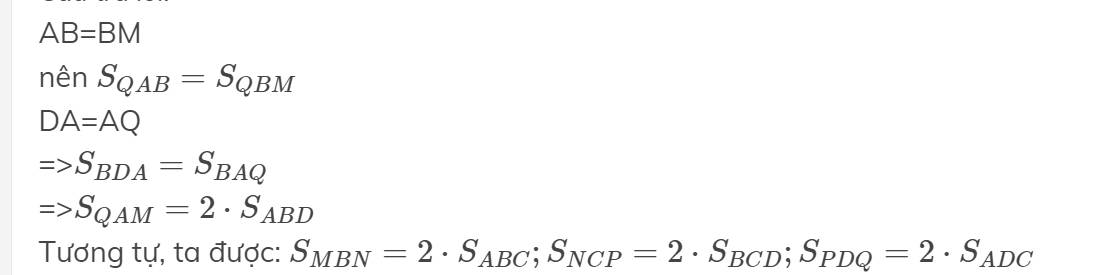
=>\(S_{MNPQ}=S_{MBN}+S_{NCP}+S_{PDQ}+S_{QMA}+S_{ABCD}\)
\(=5\cdot S_{ABCD}=5\cdot25=125\left(cm^2\right)\)