Cho đường tròn tâm O đường kính AB, E là 1 điểm trên đường tròn (O) (E không trùng với A, E không trùng với B). Gọi M, N lần lượt là trung điểm của dây AE, dây BE. Tiếp tuyến của đường trong (O) tại B cắt ON kéo dài tại D.a) Chứng minh OD vuông góc với BEb) Chứng minh tam giác BDE là tam giác cânc) Chứng minh DE là tiếp tuyến của đường tròn (O) tại Ed) Chứng minh tứ giác MONE là...
Đọc tiếp
Cho đường tròn tâm O đường kính AB, E là 1 điểm trên đường tròn (O) (E không trùng với A, E không trùng với B). Gọi M, N lần lượt là trung điểm của dây AE, dây BE. Tiếp tuyến của đường trong (O) tại B cắt ON kéo dài tại D.
a) Chứng minh OD vuông góc với BE
b) Chứng minh tam giác BDE là tam giác cân
c) Chứng minh DE là tiếp tuyến của đường tròn (O) tại E
d) Chứng minh tứ giác MONE là hcn
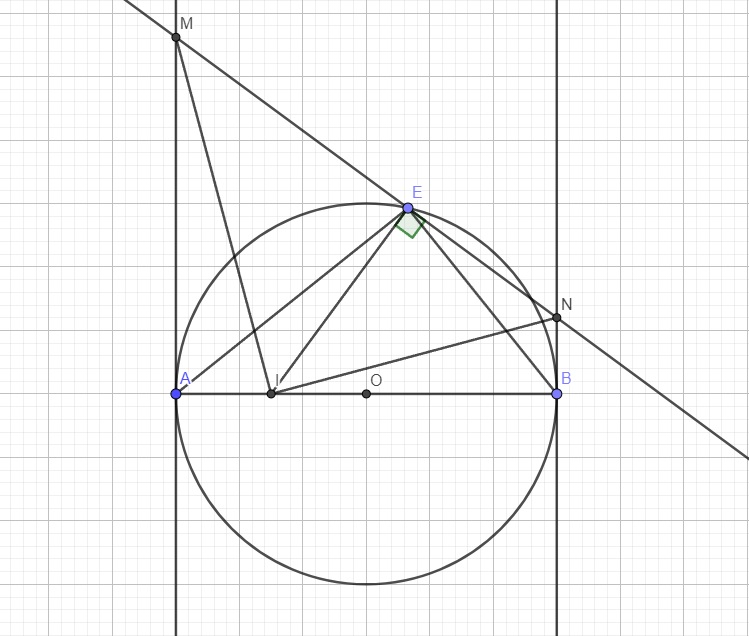
a: Ta có: ΔOBE cân tại O
mà OD là trung tuyến
nên OD vuông góc với BE và OD là phân giác của góc BOE
b: Xét ΔDEB có
DN vừa là đường cao, vừa là trung tuyến
nên ΔDEB cân tại D
c: Xét ΔDBO và ΔDEO có
DB=DE
BO=EO
DO chung
Do đo: ΔDBO=ΔDEO
=>góc DEO=90 độ
=>DE là tiếp tuyến của (O)
d: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đo: ΔAEB vuông tại E
Xét ΔAEB có AO/AB=AM/AE
nên OM//EB và OM=EB/2
=>OM//EN và OM=EN
=>EMON là hình bình hành
mà góc MEN=90 độ
nên EMON là hình chữ nhật