Cho điểm A nằm trog góc xOy( khác góc bẹt ). Vẽ điểm B so cho A là trung điểm của OB. Kẻ đường thẳng Bm//Ox, cắt Oy ở C. CA cắt Ox ở D. Chứng minh rằng: AC= AD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
a) Vì Bm // Ox nên \(\widehat{ABC}=\widehat{AOD}\) ( so le trong )
Xét \(\Delta ABC,\Delta AOD\) có:
\(\widehat{ABC}=\widehat{AOD}\left(cmt\right)\)
\(OA=AB\left(=\frac{1}{2}OB\right)\)
\(\widehat{DAO}=\widehat{BAC}\) ( đối đỉnh )
\(\Rightarrow\Delta ABC=\Delta AOD\left(g-c-g\right)\)
\(\Rightarrow AD=AC\) ( cạnh t.ứng )
b)Vì Bm // Ox nên \(\widehat{BDA}=\widehat{OCA}\) ( so le trong )
Xét \(\Delta DAB,\Delta CAO\) có:
\(\widehat{BDA}=\widehat{OCA}\left(cmt\right)\)
\(AD=AC\left(cmt\right)\)
\(\widehat{DAB}=\widehat{CAO}\) ( đối đỉnh )
\(\Rightarrow\Delta DAB=\Delta CAO\left(g-c-g\right)\)
\(\Rightarrow OC=BD\) ( cạnh t/ứng )
c) Vì \(\Delta DAB=\Delta CAO\)
\(\Rightarrow\widehat{DBA}=\widehat{AOC}\) ( góc t/ứng )
Mà 2 góc trên ở vị trí so le trong nên OC // BD
Vậy...

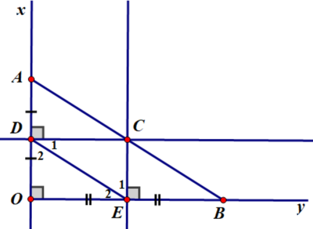
Hai tam giác vuông ΔDCE và ΔCDA có :
CD chung
CE = AD (do ∆BCE = ∆CDA)
⇒ ∆DCE = ∆CDA (hai cạnh góc vuông)


a) Xét 2 tam giác vuông OAC và tam giác OBD có:
OA = OB (gt)
O là góc chung
suy ra tam giác OAC = tam giác OBD (cạnh góc vuông - góc nhọn kề cạnh ấy)
b) Ta có : OD = OA + AD
OC = OB + BC
mà OD = OC (vì tam giác OAC = tam giác OBD)
OA = OB ( gt)
suy ra AD = BC
Xét 2 tam giác vuông ADI và tam giác BCI có:
AD = BC (cmt)
góc D = góc C (vì tam giác OAC = tam giác OBD)
suy ra tam giác ADI và tam giác BCI (cạnh goác vuông - góc nhọn kề cạnh ấy)
suy ra IA = IB (2 cạnh tương ứng)
c)Xét 2 tam giác vuông OAI và tam giác OBI có:
OI là cạnh chung
OA = OB (gt)
suy ra tam giác OAI = tam giác OBI (2 cạnh góc vuông)
suy ra góc O1 = góc O2 (2 góc tương ứng)
suy ra OI là tia phân giác của góc xOy
Cái chỗ A1, A2, B1, B2 bạn đừng kí hiệu vào bài làm nhé!
Mình nhầm tí!
Bài làm
Vì Ox // Bm
=> \(\widehat{DOA}=\widehat{ABC}\)( hai góc so le trong )
Xét tam giác DOA và tam giác CBA
Ta có: \(\widehat{DOA}=\widehat{ABC}\)( chứng minh trên )
OA = AB ( Vì A là trung điểm của OB )
\(\widehat{DAO}=\widehat{BAC}\)( hai góc đối đỉnh )
=> Tam giác DOA = tam giác mBA ( g.c.g )
=> AD = AC ( hai cạnh tương ứng )
Vậy AD = AC ( đpcm )
# Chúc bạn học tốt #