một vật có khối lượng m=50kg được kéo cho trượt đều trên mặt phẳng nằm ngang bằng 1 lực kéo F có phương tạo với phương nằm ngang góc \(\alpha\) theo hướng chếch lên trên.Hệ số ma sát trượt \(\mu\)=0.2
a. tính độ lớn của lực F với \(\alpha\) =30
b, Với giá trị nào của góc \(\alpha\) thì có giá trị nhỏ nhất tính giá trị nhỏ nhất đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
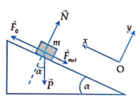
+ Khi vật trượt đều lên mặt phẳng nghiêng:
![]()
Chiếu lên phương mặt phẳng nghiêng và vuông góc với mặt phẳng nghiêng:
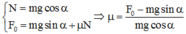
+ Khi vật trượt đều trên mặt ngang:
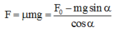

Chọn C.
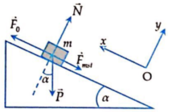
+ Khi vật trượt đều lên mặt phẳng nghiêng:
F 0 ⇀ + P ⇀ + N ⇀ + F m s ⇀ = 0 ⇀
Chiếu lên phương mặt phẳng nghiêng và vuông góc với mặt phẳng nghiêng:
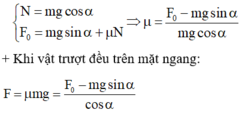

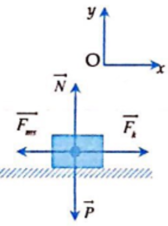
a,Gia tốc của vật
\(a=\dfrac{v-v_0}{t}=\dfrac{15-0}{30}=0,5\left(\dfrac{m}{s^2}\right)\)
b,Theo định luật II Niu tơn
\(\overrightarrow{F_k}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m\cdot\overrightarrow{a}\)
Chiếu lên trục Oy: \(N=P+F_k\cdot sin30^o=200+\dfrac{1}{2}F_k\)
Chiếu lên trục Ox:
\(cos30^o\cdot F_k-F_{ms}=m\cdot a\Rightarrow cos30^o\cdot F_k-0,25\cdot\left(200+\dfrac{1}{2}F_k\right)=20\cdot0,5\Rightarrow\)
\(\Rightarrow F_k=80,97\left(N\right)\)
\(\Rightarrow F_{ms}=60,12\left(N\right)\)

Chọn D.
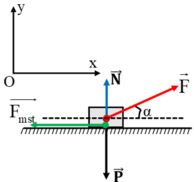
Theo định luật II Niu - tơn:
P → + N → + F k → + F m s → = m a →
Chiếu lên trục Oy:
N – P = 0 => N = P = m.g = 15.10 = 150 (N)
⇒ F m s = μ . N = 0,05.150 = 7,5 ( N )
Chiếu lên trục Ox:
F k − F m s = m . a ⇒ a = F k − F m s m = 45 − 7,5 15 = 2,5 ( m / s 2 )
Quãng đường vật đi được sau 5s là
S = 1 2 a . t 2 = 1 2 .2,5.5 = 2 31,25 m

Chọn chiều (+) là chiều chuyển động của vật.
Vật được kéo trên mặt phẳng nằm ngang \(\Rightarrow N=P=mg=15.10=150\left(N\right)\)
Lực ma sát \(F_{ms}=\mu N=0,05.150=7,5\left(N\right)\)
Áp dụng định luật II Newton, ta có \(\overrightarrow{F}=m\overrightarrow{a}\) (1)
Chiếu (1) lên phương chuyển động của vật, ta có:
\(F_k-F_{ms}=ma\Rightarrow a=\dfrac{F_k-F_{ms}}{m}=\dfrac{45-7,5}{15}=2,5\left(m/s^2\right)\)
Vậy gia tốc của thùng là \(2,5m/s^2\).

Chọn A.
Vật chuyển động thằng đều ⇒ a = 0
Theo định luật II Niu-tơn ta có:
P ⇀ + N ⇀ + P ⇀ + F m s ⇀ = 0(1)
Chọn hệ quy chiếu Oxy như hình vẽ.
Chiếu phương trình (1) lên phương thẳng đứng (Oy), ta được:
F.sin20° + N – P = 0 → N = P – F.sin20°.
Chiếu phương trình (1) lên phương ngang (Ox), ta được:
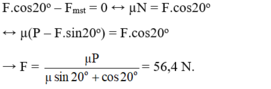
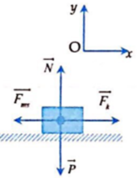
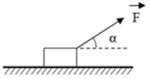
a) theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\)
chiếu lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
F.cos\(\alpha\)-\(\mu.N=0\) (1) (a=0, vật chuyển động đều)
chiếu lên trục Oy phương thẳng đứng chiều dương hướng lên trên
N=P-\(sin\alpha.F\) (2)
từ (1),(2)\(\Rightarrow F\approx103,5N\)
b) từ câu a ta có
\(F.cos\alpha-\mu.\left(P-sin\alpha.F\right)=0\)
\(\Leftrightarrow F=\dfrac{\mu.P}{cos\alpha+\mu.sin\alpha}\)
đặt \(\mu\)=\(tan\beta=\dfrac{sin\beta}{cos\beta}\) (\(0^0< \beta< 90^0\)
để F min thì MS= \(cos\alpha+\mu.sin\alpha\) max (MS: mẫu số)
\(\Leftrightarrow\)MS=\(\dfrac{cos\alpha.cos\beta+sin\beta.sin\alpha}{cos\beta}\)=\(\dfrac{cos\left(\alpha-\beta\right)}{cos\beta}\)
MS max khi \(cos\left(\alpha-\beta\right)\)=1 (vì \(cos\beta\) ở dưới mẫu min thì MS max nhưng cos\(\beta\) min ko xác định được )
\(cos\left(\alpha-\beta\right)=1\Leftrightarrow\alpha-\beta=0\)
\(\Leftrightarrow\alpha=\beta\)
\(\Rightarrow tan\alpha=tan\beta=\mu=0,2\)
\(\Rightarrow\alpha\approx11,3^0\)
F=98N