Bài 1:
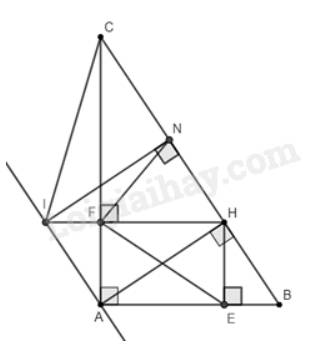
Cho \(\Delta ABC\)nhọn có AB = AC, H là trung điểm của BC. Từ H kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F.
a) CMR: \(\Delta ABH=\Delta ACH\)
b) CMR: \(\Delta AHE=\)\(\Delta AHF\)
c) Gọi M là giao điểm của đường thẳng AB và đường thẳng HF, N là giao điểm của đường thẳng AC và đường thẳng HE. CMR: \(ME=NF;MF=NE\)
d) CMR: \(ÊF//MN\)
VẼ HÌNH VÀ VIẾT GIẢ THIẾT KẾT LUẬN MIK MỚI TICK.
THANKS CÁC BN NHÌU <3