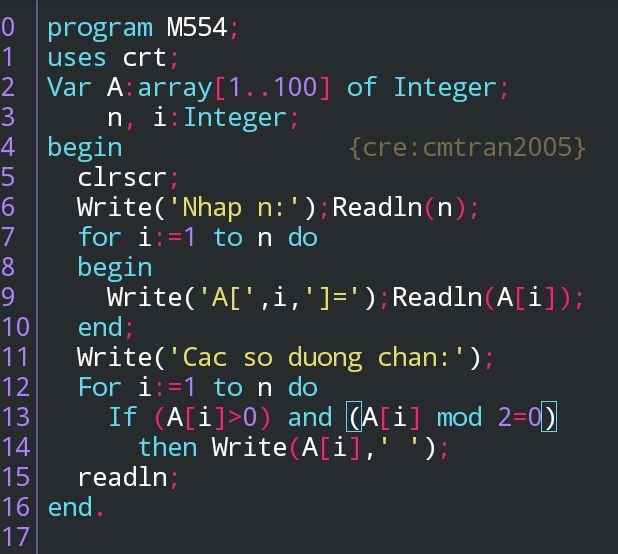
mn giúp em đc ko ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 11 2021
Bài 3:
Khi mắc nối tiếp:
\(R_{tđ}=R_1+R_2+R_3+R_4=5+10+15+20=50\left(\Omega\right)\)
\(I=I_1=I_2=I_3=I_4=\dfrac{U}{R_{tđ}}=\dfrac{20}{50}=0,4\left(A\right)\)
\(\left\{{}\begin{matrix}U_1=I_1.R_1=0,4.5=2\left(V\right)\\U_2=I_2.R_2=0,4.10=4\left(V\right)\\U_3=I_3.R_3=0,4.15=6\left(V\right)\\U_4=I_4.R_4=0,4.20=8\left(V\right)\end{matrix}\right.\)
Khi mắc song song:
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}+\dfrac{1}{R_4}=\dfrac{1}{5}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{20}=\dfrac{5}{12}\)
\(\Rightarrow R_{tđ}=2,4\left(\Omega\right)\)
\(U=U_1=U_2=U_3=U_4=20V\)
\(\left\{{}\begin{matrix}I_1=\dfrac{U_1}{R_1}=\dfrac{20}{5}=4\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{20}{10}=2\left(A\right)\\I_3=\dfrac{U_3}{R_3}=\dfrac{20}{15}=\dfrac{4}{3}\left(A\right)\\I_4=\dfrac{U_4}{R_4}=\dfrac{20}{20}=1\left(A\right)\end{matrix}\right.\)
N
6 tháng 11 2021
BÀI 3:
NỐI TIẾP:
a. \(R=R1+R2+R3+R4=5+10+15+20=50\Omega\)
b. \(I=I1=I2=I3=I4=\dfrac{U}{R}=\dfrac{20}{50}=0,4A\left(R1ntR2ntR3ntR4\right)\)
c. \(\left\{{}\begin{matrix}U1=I1.R1=0,4.5=2A\\U2=I2.R2=0,4.10=4A\\U3=I3.R3=0,4.15=6V\\U4=I4.R4=0,4.20=8V\end{matrix}\right.\)
SONG SONG:
a. \(\dfrac{1}{R}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}+\dfrac{1}{R4}=\dfrac{1}{5}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{20}=\dfrac{5}{12}\Rightarrow R=2,4\Omega\)
c. \(U=U1=U2=U3=U4=20V\left(R1\backslash\backslash\mathbb{R}2\backslash\backslash\mathbb{R}3\backslash\backslash R4\right)\)
b. \(\left\{{}\begin{matrix}I1=U1:R1=20:5=4A\\I2=U2:R2=20:10=2A\\I3=U3:R3=20:15=\dfrac{4}{3}A\\I4=U4:R4=20:20=1A\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 1 2022
Tịnh tiến đồ thị vế phía trái \(x_1+1\) đơn vị độ dài (trung điểm \(x_1;x_2\) trùng gốc tọa độ) \(\Rightarrow\) hai cực trị của hàm số lúc này là -1 và 1
\(\Rightarrow y'=0\) có 2 nghiệm \(\pm1\Rightarrow f'\left(x\right)=a\left(x^2-1\right)\Rightarrow f\left(x\right)=\dfrac{a}{3}\left(x^3-3x\right)\)
\(\int\limits^0_{-1}f\left(x\right)dx=\dfrac{5}{4}\Rightarrow\int\limits^0_{-1}\dfrac{a}{3}\left(x^3-3x\right)=\dfrac{5}{4}\Rightarrow\dfrac{a}{3}.\dfrac{5}{4}=\dfrac{5}{4}\Rightarrow a=3\)
\(\Rightarrow f\left(x\right)=x^3-3x\Rightarrow L=\lim\limits_{x\rightarrow-1}\dfrac{x^3-3x-2}{\left(x+1\right)^2}=\lim\limits_{x\rightarrow-1}\left(x-2\right)=-3\)
GL
0
DT
31 tháng 1 2022
Do \(M\in d\) nên M(1+2t; 1-t ; t)
MA+MB= \(\sqrt{4t^2+\left(t-1\right)^2+\left(t+1\right)^2}+\sqrt{\left(2t-1\right)^2+t^2+\left(t-1\right)^2}\)
\(=\sqrt{6t^2+2}+\sqrt{6t^2-6t+2}=\sqrt{6t^2+2+}\sqrt{6.\left(t-\dfrac{1}{2}\right)^2+\dfrac{1}{2}}\)
Chọn \(\overset{r}{u}=\left(\sqrt{6t};\sqrt{2}\right);\overset{r}{v}=\left(\sqrt{6}.\left(\dfrac{1}{2}-t\right);\dfrac{1}{\sqrt{2}}\right)\)
\(\Rightarrow\overset{r}{u}+\overset{r}{v}=\left(\dfrac{\sqrt{6}}{2};\dfrac{3}{\sqrt{2}}\right)\) , Ta có :
MA+MB=\(\left|\overset{r}{u}\right|+\left|\overset{r}{v}\right|\ge\left|\overset{r}{u}+\overset{r}{v}\right|=\sqrt{\dfrac{6}{4}+\dfrac{9}{2}}=\sqrt{6}\)
Dấu đẳng thức xảy ra <=> \(\overset{r}{u};\overset{r}{v}\) cùng hướng
\(\Leftrightarrow\dfrac{\sqrt{6t}}{\sqrt{6}\left(\dfrac{1}{2}-t\right)}=\dfrac{\sqrt{2}}{\dfrac{1}{\sqrt{2}}}\Leftrightarrow1=1-2t\)
\(\Leftrightarrow t=\dfrac{1}{3}\) . Vậy MA+MB nhỏ nhất
\(\Leftrightarrow M\left(\dfrac{5}{3},\dfrac{2}{3};\dfrac{1}{3}\right)\)
Vậy chọn D
E
1 tháng 2 2022
(SAB) và (SCD) có AB // CD => giao tuyến của chúng là 1 đường thẳng song song với AB và CD
Mà SD vuông góc với CD; SA vuông góc với AB nên góc giữa 2 mp (SAB) và (SCD) là góc giữa SA và SD hay là góc ASD
tan \(\widehat{ASD}\) = \(\dfrac{AD}{SA}\) = \(\dfrac{1}{\sqrt{3}}\)
=> \(\widehat{ASD}=30^{^o}\)
DT
31 tháng 1 2022
+ số phần tử của không gian mẫu là: \(n\left(\pi\right)=C\overset{1}{6}.C\overset{1}{6}=36\)
+ gọi A bằng " Cả 2 lần xuất hiện mặt 6 chấm "
số phần tử của biến cố A là n(A) =1
Xác xuất biến cố A là P(A) = \(\dfrac{n\left(A\right)}{n\left(\pi\right)}=\dfrac{1}{36}\)
Vậy chọn A