- các bạn có thể chỉ cho mình cách học toán tốt không
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các phương pháp học toán để giỏi
Học cách ghi nhớ các công thức và lý thuyết môn toán
Bạn nên dành ít nhất 60 phút mỗi ngày để học các công thức Toán học, cho đến khi bạn tin chắc những công thức đó đã nằm gọn trong đầu bạn thì bạn vẫn phải ôn lại chúng mỗi ngày. Hãy bắt đầu bằng việc học lại các công thức đơn giản nhất, làm lại các bài tập với các phép tính đơn giản nhất, hãy bắt đầu lại với: cộng, trừ, nhân, chia…Có thể bạn sẽ không tin, nhưng nếu bạn làm đi làm lại những công thức này nhiều lần chúng sẽ tự động được cài vào bộ nhớ của não bạn, đều này có lợi rất lớn cho bạn trong những bài tập sau này. Tiếp đến, hãy tập làm quen với những công thức khó, không gì tốt hơn cho sự ghi nhớ là học đi học lại nhiều lần .
Hãy làm bài tập nhiều
Để học tốt môn Toán, bạn không thể bỏ qua việc làm các bài tập. Làm nhiều lần, làm nhiều dạng, cùng một bài nhưng áp dụng nhiều phương pháp khác nhau để cuối cùng tìm ra phương pháp tối ưu nhất. Khi bạn thật sự hứng thú với việc giải các bài Toán thì việc giải được một bài Toán khó sẽ giúp bạn cảm thấy thực sự hứng khởi, hào hứng, nó cũng là động lực giúp bạn “chinh phục” các bài Toán khó khác
Học nhóm
Có thể bạn rất giỏi ở một môn học nào đó, nhưng lại học rất tệ môn khác. Học nhóm là cách rất tốt để những người bạn có thể bổ sung ưu điểm, hạn chế khiếm khuyết cho nhau. Đối với việc học Toán cũng vậy, các bạn có thể cùng nhau lập thành một nhóm để cùng nhau học Toán. Tuy nhiên, để cho việc học nhóm hiệu quả trước tiên mỗi thành viên phải tự giải các bài Toán, sau đó mới cùng nhau lựa chọn một cách giải đơn giản và dễ hiểu nhất. Tức là dù học nhóm thì tất cả các bạn đều phải làm việc cách tích cực, không nên ỉ lại người khác.
Tạo niềm hăng say với môn học
Với nhiều người, Toán học là một môn học vô cùng khô khan và cứng nhắc bởi vậy việc tạo niềm say mê với môn học là đều không dễ. Tuy vậy, bạn vẫn có thể tìm thấy niềm vui từ việc học Toán nếu bạn thật sự yêu thích nó. Toán học không hề khô khan, bạn vẫn có thể làm thơ, làm vè từ những công thức Toán để dễ nhớ, dễ học. Đồng thời, khi đang giải một bài tập đặc biệt là những bài tập khó bạn nên chú tâm vào nó và đừng để ý đến những thứ xung quanh. Việc tập trung hết năng lực để giúp bạn đạt hiệu quả cao hơn.
Tránh học dồn
Một đều bạn nên nhớ đối với việc học Toán là không để dồn các bài tập, các công thức lại để làm và học một lần. Bởi lẽ, Toán học là một chuỗi liên kết các công thức, các bài tập. Nó giống như việc xây nhà, nếu bạn muốn xây tầng 2 bạn sẽ phải xây móng thật vững, tiếp đến là tầng trệt, rồi mới tiếp tục xây lên, các công đoạn phải được thực hiện trước sau rõ ràng. Bởi vậy, đối với việc học Toán nói riêng và tất cả các môn học khác nói chung bạn không nên và không được phép học dồn. Đều đó sẽ khiến bạn bị mất nền tảng, và lấy đi của bạn rất nhiều thời gian. Nếu để đến thi mới học thì bạn sẽ không thể học kịp và điểm số của bạn rất thấp trong kì thi là đều tất nhiên.
Toán học không khó, cái khó là bạn không chịu thay đổi suy nghĩ của mình với nó. Toán học rất cần thiết cho cuộc sống của chúng ta, bởi vậy, thay vì lẫn tránh nó chúng ta hãy học cách làm quen với nó. Trên đây là một số phương pháp để có thể học giỏi môn Toán. Hy vọng các bạn sẽ tiếp thu được ít nhiều kiến thức có được trong bài viết._Chúc bạn học thật tốt_
Dành đủ thời gian cần thiết
Để trở thành học sinh giỏi toán trong lớp chả có gì khó khăn. Bởi kiến thức trong sách giáo khoa là dành cho tất cả mọi người. Bạn ơi! Nó không phải là ngành khoa học chế tạo tên lửa. Vì thế, tin mình đi! Bạn chỉ cần dành đủ giờ ngồi “cày hết đống bài tập” bạn tự khắc sẽ giỏi lên ngay thôi. Cũng như chơi game vậy, bạn sẽ tích lũy được điểm kinh nghiệm thông qua các bài tập và đương nhiên sẽ lên . Bạn sẽ tự cảm nhận được sự tiến bộ của mình sau từng tuần và khi đến bài kiểm tra bạn sẽ thấy điều kỳ diệu.
Kiên nhẫn chờ thành quả
Hãy kiên nhẫn liên tục lặp lại bước 1 và 2. Hãy để cho các bạntrong phòng học thấy bạn như là một học sinh năng động nhất lớp học. Đầy hào hứng và mặc dù đôi khi xung phong lên giải bài mà vẫn sai. Không có gì nghiêm trọng cả khi đến bài kiểm tra bạn sẽ làm đúng. Hãy dành riêng cho việc học toán một khoảng thời gian cố định. Có thể mỗi ngày 45 phút đến 1 tiếng: đều đặn và cần mẫn.mình xin nhấn mạnh từ khóa quan trọng ở đây là sự đều đặn. Và chỉ cần trong 1-2 tuần bạn đã cảm nhận sự khác biệt.
Mọi thứ sẽ dễ dàng hơn khi bạn bắt đầu thấy điểm kiểm tra tăng dần. Bạn hình dung được cảm giác đó không. Điểm 9,5 toán đầu tiên trong suốt 2 tháng qua. Thực sự không thể tin nổi. Và đến lúc này bạn chẳng cần phải thực hiện bước 1 nữa. Vì bạn đã thực sự thích môn toán hơn rồi.
tk nhá

Cách học tốt toán theo ý mình là:
-Bạn nên lấy một tấm bài cứng ghi công thức hay lý thuyết gì đó lên,cứ mỗi ngày bạn đọc vài lần,dần dần sẽ thuộc.
-Bạn nên chú ý nghe thầy giảng bài thật kĩ.Đừng lơ là.

- Học theo thơ nhé. Mình lấy 2 bài này cho cậu tham khảo đã nhé;
+ Bài cơ bản:
Kali (K) , iot (I) , hidrô (H)
Natri (Na) với Bạc (Ag) , Clo (Cl) một loài
Là hoá trị I hởi ai!
Nhớ ghi cho kỉ khỏi hoài phân vân...
Magiê (Mg) kẽm (Zn) với thuỷ ngân (Hg)
Oxi (O) , đồng (Cu) , thiếc (Sn) thêm phần Bari (Ba)
Cuối cùng thêm chú Canxi (Ca)
Hoá trị II nhớ có dzì khó khăn !
Này nhôm hoá trị III lần.
In sâu trí nhớ khi cần có ngay.
Cacbon © , silic (Si) này đây
Có hoá trị IV không ngày nào quên.
Sắt (Fe) lắm lúc hay phiền?
II , III lên xuống nhớ liền ngay thôi.
Lại gặp nitơ (N) khó rồi
I , II , III , IV khi thời lên V.
Lưu huỳnh (S) lắm lúc chơi khăm
Xuống II lên IV khi nằm thứ V.
Phot pho (P) nói đến ko dư
Có ai hỏi đến thì ừ rằng V.
Em ơi , cố gắng học chăm
Bài ca hoá trị suốt năm cần dùng
+ Bài nâng cao:
Hidro (H) cùng với liti (Li)
Natri (Na) cùng với kali (K) chẳng rời
Ngoài ra còn bạc (Ag) sáng ngời
Chỉ mang hoá trị I thôi chớ nhầm
Riêng đồng (Cu) cùng với thuỷ ngân (Hg)
Thường II ít I chớ phân vân gì
Đổi thay II , IV là chì (Pb)
Điển hình hoá trị của chì là II
Bao giờ cùng hoá trị II
Là ôxi (O) , kẽm(Zn) chẳng sai chút gì
Ngoài ra còn có canxi (Ca)
Magiê (Mg) cùng với bari (Ba) một nhà
Bo (B) , nhôm (Al) thì hóa trị III
Cácbon © silic (Si) thiếc (Sn) là IV thôi
Thế nhưng phải nói thêm lời
Hóa trị II vẫn là nơi đi về
Sắt (Fe) II toan tính bộn bề
Không bền nên dễ biến liền sắt III
Phốtpho III ít gặp mà
Photpho V chính người ta gặp nhiều
Nitơ (N) hoá trị bao nhiêu ?
I , II, III , IV phần nhiều tới V
Lưu huynh lắm lúc chơi khăm
Khi II lúc IV , VI tăng tột cùng
Clo Iot lung tung
II III V VII thường thì I thôi
Mangan rắc rối nhất đời
Đổi từ I đến VII thời mới yên
Hoá trị II dùng rất nhiều
Hoá trị VII cũng được yêu hay cần
Bài ca hoá trị thuộc lòng
Viết thông công thức đề phòng lãng quên
Học hành cố gắng cần chuyên
Siêng ôn chăm luyện tất nhiên nhớ nhiều.
- Chúc bạn học tốt ![]()
Miamoto Shizuka mỗi ngày hc thuộc hết 5 nguyên tố kèm hóa trị, kí hiệu. nguyên tử khối

bạn tham khảo 1 số đề dưới đây nha ,mình thấy khá hay và dễ
~~chúc bạn làm bài tốt~~
Đề kiểm tra 1:
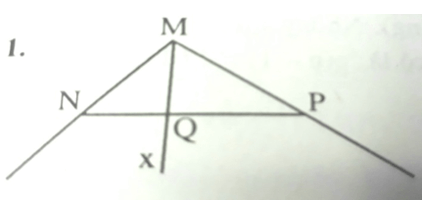
Bài 1. (2 điểm) Lấy 3 điểm không thẳng hàng M , N, P. Vẽ hai tia MN, MP sau đó vẽ tia Mx cắt đoạn thẳng NP tại Q nằm giữa N, P.
Bài 2. (3 điểm) Điểm M nằm giữa hai điểm A và B; điểm C nằm giữa hai điểm A và M, điểm D nằm giữa hai điểm M và B.
a) Tia MC trùng với tia nào? Vì sao ?
b) Tia MD trùng với tia nào? Vì sao ?
c) Điểm M có nằm giữa hai điểm C và D không? Vì sao?
Bài 3. (1 điểm) Cho trước một số điểm. Cứ qua hai điểm vẽ một đoạn thẳng. Biết rằng có 55 đoạn thẳng. Hỏi có bao nhiêu điểm cho trước?
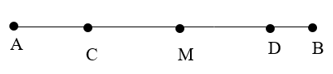
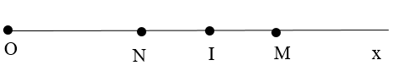
Bài 4. (4 điểm) Trên tia Ox lấy hai điểm M, N sao cho OM = 8 cm, ON = 4 cm. Gọi I là trung điểm MN.
a) Chứng tỏ rằng N là trung điểm của đoạn thẳng OM.
b) Tính IM
Đáp án và Hướng dẫn giải
Bài 1.
Bài 2.
a) Vì C nằm giữa A, M nên hai tia MA , MC trùng nhau.
b) Vì D nằm giữa M, B nên hai tia MD , MB trùng nhau.
c) Vì M nằm giữa A, B nên hai tia MA , MB đối nhau. Mà hai tia MC, MA trùng nhau, hai tia MD, MB trùng nhau. Do vậy hai tia MC, MD đối nhau
Suy ra điểm M nằm giữa C và D.
Bài 3.
Gọi số điểm cho trước là n (n ∈ N*)
Vẽ từ 1 điểm bất kì với n – 1 điểm còn lại, ta được n – 1 đoạn thẳng.
Với n điểm, nên có n(n – 1) (đoạn thẳng). Nhưng mỗi đoạn thẳng đã được tính 2 lần. Do đó số đoạn thẳng thực sự có là: n(n – 1) : 2 (đoạn thẳng)
Theo đề bài ta có:
n(n – 1) : 2 = 55
n(n – 1) = 55 . 2
n(n – 1) = 110
n(n – 1) = 11 . 10
n = 11
Vậy có 11 điểm cho trước
Bài 4.
a) Trên tia Ox có M, N và ON < OM (vì 4 cm < 8 cm ), nên N nằm giữa O và M
Do đó ON + MN = OM
4 + MN = 8
MN = 8 – 4 = 4 (cm)
Vì N nằm giữa O và M và ON = MN ( =4cm ) nên N là trung điểm của đoạn thẳng OM.
b) I là trung điểm của đoạn thẳng MN nên
Đề kiểm tra 2 :
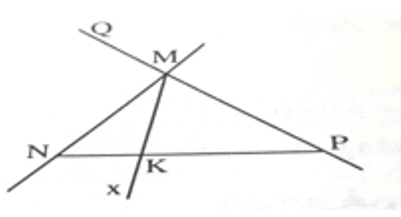
Bài 1. (2 điểm) Vẽ hình theo trình tự sau:
Cho ba điểm M, N,P không thẳng hàng
- Vẽ tia MP, đoạn thẳng NP và đường thẳng MN
- Vẽ tia MQ là tia đối của tia MP
- Vẽ tia Mx cắt đoạn thẳng NP tại K
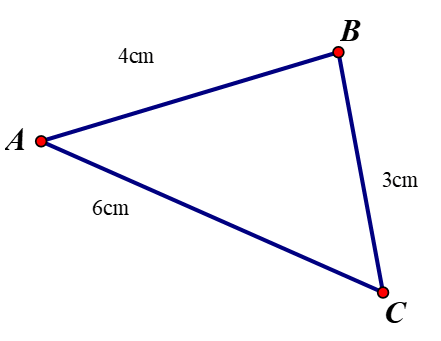
Bài 2. (3 điểm) Cho 3 điểm A, B, C biết: AB = 4cm, BC = 3 cm, AC = 6 cm. Chứng tỏ rằng:
a) Trong 3 điểm A, B, C không có điểm nào nằm giữa hai điểm còn lại
b) Ba điểm A, B, C không thẳng hàng
Bài 3. (5 điểm)
Trên tia Ax lấy các điểm B, C sao cho AB = 4 cm, AC = 8cm
a) Trong ba điểm A, B, C điểm nào nằm giữa hai điểm còn lại? Vì sao?
b) Chứng tỏ B là trung điểm của đoạn thẳng AC
c) Gọi D là trung điểm đoạn thẳng AB. Tính độ dài đoạn thẳng DC.
Đáp án và Hướng dẫn giải
Bài 1.
Bài 2.
a) Ta có: AB + BC = 4 +3 = 7 (cm), AC = 6 cm.
Nên AB + BC ≠ AC. Vậy điểm B không nằm giữa A, C.
Ta có: AB + AC = 4 + 6 = 10 (cm), BC = 3 cm.
Nên AB + AC ≠ BC. Vậy điểm A không nằm giữa B, C.
Ta có: AC + BC = 6 + 3 = 9 (cm), AB = 4 cm.
Nên AC + BC ≠ AB. Vậy điểm C không nằm giữa A, B.
b) Trong ba điểm A, B, C không có điểm nào nằm giữa hai điểm còn lại.
Vậy ba điểm A, B, C không thẳng hàng.
Bài 3.
a) Trên tia Ax có B, C và AB < AC (vì 4 cm < 8 cm ), nên B nằm giữa A và C.
b) B nằm giữa A và C nên : AB + BC = AC
4 + BC = 8
BC = 8 – 4 = 4 (cm)
Ta có B nằm giữa A và C và AB = BC = 4 cm nên B là trung điểm của đoạn thẳng AC
c) D là trung điểm của đoạn thẳng AB nên:
D là trung điểm của AB; B nằm giữa A và C nên D nằm giữa A và C
Do đó: AD + DC = AC
2 + DC = 8
DC = 8 – 2 = 6 (cm)
Đề kiểm tra 3:
Bài 1. (4 điểm) Cho 3 điểm A, B , C không thẳng hàng. Hãy vẽ đoạn thẳng BC, tia AB và đường thẳng CA.
Bài 2. (6 điểm) Trên tia Ox lấy hai điểm A, B sao cho OA = 3 cm, OB = 7 cm
a) Tính AB
b) Gọi C là trung điểm AB. Tính AC
Đáp án và Hướng dẫn giải
Bài 1.
Bài 2.
a) Trên tia Ox có A, B và OA < OB (vì 3 cm < 7 cm ), nên A nằm giữa O và B
Do đó OA + AB = OB
3 + AB = 7
AB = 7 – 3 = 4 (cm)
b) C là trung điểm của đoạn thẳng AB
Đề kiểm tra 4:
Bài 1. (2 điểm) Trên đường thẳng d lấy ba điểm E, Q, S theo thứ tự đó.
a) Hỏi có mấy đoạn thẳng tất cả, hãy kể tên các đoạn thẳng đó
b) Viết tên hai tia đối nhau gốc Q.
Bài 2. (2 điểm) Cho trước 4 điểm A, B, C, D trong đó không có 3 điểm nào thẳng hàng. Tìm điểm E sao cho A, E, B thẳng hàng và C, E, D thẳng hàng.
Bài 3. (3 điểm) Cho ba điểm M, N, P thẳng hàng, điểm M không nằm giữa hai điểm N và P. Biết: MN = 6 cm, MP = 2 cm. Tính PN.
Bài 4. (3 điểm) Trên tia Ox, vẽ hai điểm A, B sao cho OA = 3 cm, OB = 6 cm.
a) So sánh OA và AB.
b) Điểm A có là trung điểm của đoạn thẳng OB không? Vì sao ?
Đáp án và Hướng dẫn giải
Bài 1.
a) Có 3 đoạn thẳng đó là: RQ, QS, RS
b) Hai tia đối nhau gốc Q là: tia QR và tia QS
Bài 2.
Vẽ hai đường thẳng AB và CD cắt nhau tại E
Điểm E là điểm cần tìm
Trường hợp AB và CD không cắt nhau thì không tìm được điểm E
Bài 3.
Nếu điểm N nằm giữa hai điểm M, P thì:
MN + NP = MP
6 + NP = 2 (vô lí)
Do vậy N không nằm giữa M, P. Theo đề bài thì M không nằm giữa N và P và M, N, P thẳng hàng. Vậy P nằm giữa M và N.
⇒ MP + PN = MN
⇒ PN = MN – MP = 6 – 2 = 4 (cm)
Bài 4.
a) Trên tia Ox có A, B và OA < OB (vì 3 cm < 6 cm ), nên A nằm giữa O và B
Do đó OA + AB = OB
3 + AB = 6
AB = 6 – 3 = 3 (cm)
Vậy: OA = AB = 3 (cm)
b) Điểm A nằm giữa O, B và OA = AB. Vậy A là trung điểm của đoạn thẳng OB


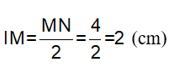

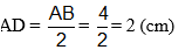

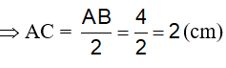


*Tham khảo nha*
1. Nhớ công thức, lý thuyết
Để học giỏi môn toán phải dành thời gian nhiều để học, mạc dù không phải học thuộc nhiều nhưng phải nhớ các định nghĩa, lý thuyết các tính chất và hệ quả.
2. Làm nhiều bài tập
Như những môn xã hội thì bạn phải dành thời gian nhiều để học thuộc thì với môn toán, phải dành nhiều thời gian để làm bài tập, đó là cách giúp bạn dễ nhớ và hiểu sâu sắc các định nghĩa và công thức. Để hiểu được một cuốn sách toàn ta cần hiểu từng trang ể hiểu hết 1 cuốn sách toán ta cần hiểu từng trang, để hiểu hết 1 trang ta chỉ cần hiểu từng dòng và để hiểu mỗi dòng có lẽ là không khó lắm. Thật ra học toán là chúng ta học tại sao có dấu bằng ? Tại sao có dấu lớn hơn ? Tại sao có dấu nhỏ hơn? Tại sao có dấu suy ra và tại sao có dấu tương đương ? Để hiểu một bài toán ta cần phải nhớ các kiến thức căn bản chứa đựng trong định nghĩa và định lý. (Để nhớ các định nghĩa và định lý ta cần làm nhiều bài tập).
3. Tự học
Tự học là cách học toán tốt nhất giúp hiểu rỏ từng vấn đề và từng trường hợp có thể xảy ra, khi chúng ta nghe giảng thì hiểu nhưng không làm lại được, vì vậy để có kiến thức chắc, phải tự làm lại bài tập từ dễ đến khó. Hãy kiến nhẫn học những kiến thức từ cơ bản đến nâng cao. Chính những bài toán đơn giản giúp ta hiểu được những kiến thức nâng cao sau này. Một bài toán khó là sự tổng hợp từ nhiều bài toán đơn giản, do đó chỉ cần nắm vững bài toán căn bản giúp dễ dàng giải quyết những bài toàn khó.
4. Yêu thích môn học
Làm gì cũng vậy, nếu có đam mê sẽ có quyết tâm và cố gắng hơn. Trong tính toán, đôi khi gặp khó khăn có thể nản lòng, nhưng nếu yêu thích nó, bạn sẽ vượt qua được. Không giải được 1 bài toán thì không yên tâm, thậm chí đến lúc ăn, lúc ngủ vẫn nghĩ cách giải. Nếu như vậy, chẳng mấy chốc bạn sẽ tìm ra được lời đáp.
5. Không học dồn
Một điều khá kiêng kị trong học Toán đó là học dồn. Để học tốt buộc bạn phải học từ đầu năm và chạy theo chương trình. Trong toán học có nhiều sự liên quan, liên kết giữa các bài học, các chương và các công thức. Muốn học tốt cái sau bạn nên nắm vững cái trước. Có như thế mới tiến bộ được. Để đạt được điểm cao cần tránh học dồn trước lúc thi, vừa căng thẳng, vừa hại sức khỏe.
Hok tốt!~
Hi bạn!
Muốn học toán tốt rất dễ
+ Thuộc hết các tính chất
+ Có đầu óc tư duy
+ chăm chú nghe thầy cô giảng bài
...............