ABCD là hình vuông có cạnh là 6(cm)
B là TĐ của AC
A: Tính diện tích của ACEG
B: Tính diện tích của tam giác ABC
C: Tính diện tích của tam giác GEF
D: Tính diện tích của BCEG
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

E là một điểm chính giữa cạnh AB nên E chính là trung điểm của cạnh AB nên AE = EB = \(\frac{AB}{2}\) = \(\frac{10}{2}\) = 5
H chính là điểm chính giữa cạnh BC nên H chính là trung điểm cạnh BC nên BH = CH = \(\frac{BC}{2}\) = \(\frac{10}{2}\) = 5
a ) Diện tích hình tam giác ADE là :
AE x AD : 2 = 25 ( cm2 )
b ) Hình thang BHDA là :
( BH + AD ) x AB : 2 = 75 ( cm2 )
c ) Diện tích hình tam giác AHE là :
AB x BH : 2 = 25 ( cm2 )
Đáp số : a ) 25 cm2
b ) 75 cm2
c ) 25 cm2

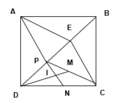
Vẽ hình đúng
a) Tính đúng diện tích hình vuông ABCD
b)-Lập luận đúng diện tích các tam giác ADP, APE, AEB, CPD, CPE, CEB bằng nhau và bằng 1 6 diện tích hình vuông ABCD.
-Lập luận được diện tích hình AECP bằng 1 3 diện tích hình vuông ABCD
-Tính đúng kết quả 12cm2
c)- Lập luận đúng diện tích tam giác DPM và DPN bằng nhau
- Lập luận đúng diện tích tam giác PMI và DNI bằng nhau

1. Cạnh đáy của hình tam giác là:
\(27:\left(\frac{1}{2}x4,5\right)=12\)(cm)
2.

Từ đề bài, ta suy ra tỉ lệ các diện tích là:
SBAE = SACE = SMAC = SMBC
Độ dài AB là: 54 : (12 : 2) = 9 (cm)
Xét 2 tam giác MAC và ACE: Do đều có diện tích như nhau (cả 2 đều chiếm \(\dfrac{1}{2}\) diện tích ABC), chung tam giác AIC.
⇒ SAMI = SEIC
Nối B tới I, ta có được tam giác MBC được chia thành 3 phần bằng nhau ⇒ Mỗi phần sẽ có diện tích là: 27 : 3 = 9 (cm2)
Diện tích tam giác AIC là: 54 - 27 - 9 = 18 (cm2)
Độ đường cao IK là: 18 : (12 : 2) = 3 (cm)
Đáp số: a) 9cm
b) SAMI = SEIC
c) 3cm