quy đồng mẫu thức các phân thức : a/ x-1/ x^3 + 1 ; 2x/x^2 - x + 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a: \(\dfrac{1}{2x^3y}=\dfrac{6yz^3}{12x^3y^2z^3}\)
\(\dfrac{2}{3xy^2z^3}=\dfrac{2\cdot4x^2}{12x^3y^2z^3}=\dfrac{8x^2}{12x^3y^2z^3}\)

a: 1/x^2y=1/x^2y
3/xy=3x/x^2y
b: \(\dfrac{x}{x^2+2xy+y^2}=\dfrac{x}{\left(x+y\right)^2}\)
\(\dfrac{2x}{x^2+xy}=\dfrac{2}{x+y}=\dfrac{2x+2y}{\left(x+y\right)^2}\)


x − 2 3 x − 1 = 2 x + 1 x − 2 3.2 x + 1 x − 1 = 2 x − 2 6 x 2 − 1



MTC : ( x - 1 )( x2 + x + 1 )
Ta có : \(\frac{4x^2-3x+5}{x^3-1}=\frac{4x^2-3x+5}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{2x}{x^2+x+1}=\frac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{2x^2-2x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{6}{x-1}=\frac{6\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{6x^2+6x+6}{\left(x-1\right)\left(x^2+x+1\right)}\)
Hnay mới học thì hnay trả lời nhá :P
\(\frac{4x^2-3x+5}{x^3-1};\frac{2x}{x^2+x+1}\)
Ta có : \(x^3-1=\left(x-1\right)\left(x^2+x+1\right)\)
\(x^2+x+1=x^2+x+1\)
MTC : \(\left(x-1\right)\left(x^2+x+1\right)\)
\(\frac{4x^2-3x+5}{x^3-1}=\frac{4x^2-3x+5}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{2x}{x^2+x+1}=\frac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{2x^2-2x}{\left(x-1\right)\left(x^2+x+1\right)}\)
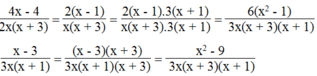
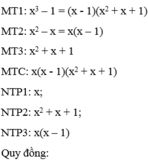
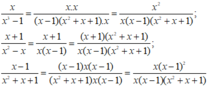


\(\dfrac{x-1}{x^3+1}=\dfrac{\left(x-1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(\dfrac{2x}{x^2-x+1}=\dfrac{2x\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{2x^2+2x}{\left(x+1\right)\left(x^2-x+1\right)}\)