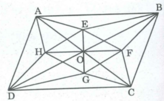
cho hình bình hành ABCD hai đường chéo cắt nhau tại O hai đường cao AM DN của tam giác AOD cắt nhau tại E 2 đường cao CP BQ của tam giác BOC cắt nhau tại F chứng minh
a) AMCP MNPQ là hình bình hành
b) O là trung điểm của EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 11 2021
a: Xét ΔAMO vuông tại M và ΔCPO vuông tại P có
OA=OC
\(\widehat{AOM}=\widehat{COP}\)
Do đó: ΔAMO=ΔCPO
Suy ra: OM=OP
hay O là trung điểm của PM
Xét ΔDQO vuông tại Q và ΔBNO vuông tại N có
OD=OB
\(\widehat{DOQ}=\widehat{BON}\)
Do đó: ΔDQO=ΔBNO
Suy a: OQ=ON
hay O là trung điểm của QN
Xét tứ giác AMCP có
O là trung điểm của AC
O là trung điểm của MP
Do đó: AMCP là hình bình hành
Xét tứ giác MNPQ có
O là trung điểm của MP
O là trung điểm của NQ
Do đó: MNPQ là hình bình hành
CM
7 tháng 10 2018
Ta có: ∠ (AOB) = ∠ (COD) (đối đỉnh)
∠ (EOB ) = 1/2 ∠ (AOB) (gt)
∠ (COG) = 1/2 ∠ (COD) (gt)
Suy ra: ∠ (EOB ) = ∠ (COG)
∠ (EOB) + ∠ (BOC) + ∠ (COG) = 2 ∠ (EOB) + ∠ (BOC)
Mà ∠ (AOB ) + ∠ (BOC) = 180 0 ( kề bù).Hay 2 ∠ (EOB) + ∠ (BOC ) = 180 0
Suy ra: E,O,G thẳng hàng
Ta lại có: ∠ (BOC) = ∠ (AOD ) ( đối đỉnh)
∠ (HOD) = 1/2 ∠ (AOD) (gt)
∠ (FOC) = 1/2 ∠ (BOC) (gt)
Suy ra: ∠ (HOD) = ∠ (FOC)
∠ (HOD) + ∠ (COD ) + ∠ (FOC) = 2 ∠ (HOD) + ∠ (COD)
Mà ∠ (AOD) + ∠ (COD) = 180 0 ( kề bù). Hay 2 ∠ (HOD) + ∠ (COD) = 180 0
Suy ra: H, O, F thẳng hàng
∠ (ADO) = ∠ (CBO) ( so le trong)
∠ (HDO) = ∠ (FBO) ( chứng minh trên)
OD = OB ( t/chất hình bình hành)
∠ (HOD) = ∠ (FOB ) ( đối đỉnh)
Do đó: ∆ BFO = ∆ DHO (g.c.g)
⇒ OF = OH
∠ (OAB) = ∠ (OCD) ( so le trong)
∠ (OAE) = 1/2 ∠ (OAB ) (gt)
∠ (OCG) = 1/2 ∠ (OCD) (gt)
Suy ra: ∠ (OAE) = ∠ (OCG)
Xét ∆ OAE và ∆ OCG,ta có :
∠ (OAE) = ∠ (OCG) ( chứng mình trên)
OA = OC ( t/chất hình bình hành)
∠ (EOA) = ∠ (GOC) ( đối đỉnh)
Do đó: ∆ OAE= ∆ OCG (g.c.g) ⇒ OE = OG
Suy ra tứ giác EFGH là hình bình hành ( vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
OE ⊥ OF (tính chất tia phân giác của hai góc kề bù) hay EG ⊥ FH
Vậy tứ giác EFGH là hình thoi
ai giúp mình với
a: Xét ΔADM vuông tại M và ΔCBP vuông tại P có
AD=CB
góc ADM=góc CBP
Do đó: ΔADM=ΔCBP
=>AM=CP
Xét tứ giác AMCP có
AM//CP
AM=CP
Do đó: AMCP là hình bình hành
=>AC cắt PM tại trung điểm của mỗi đường
=>O là trung điểm của PM
Xét ΔOND vuông tại N và ΔOQB vuông tại Q có
OD=OB
góc NOD=góc QOB
Do đó: ΔOND=ΔOQB
=>DN=QB
Xét tứ giác DNBQ có
DN//BQ
DN=BQ
DO đó: DNBQ là hình bình hành
Suy ra: DB cắt NQ tại trung điểm của mỗi đường
=>O là trung điểm của NQ
Xét tứ giác MNPQ có
O là trung điểm chung của MP và NQ
nên MNPQ là hình bình hành
b: Xét ΔANE vuông tại N và ΔCFQ vuông tại Q có
NA=CQ
góc NAE=góc FCQ
Do đó: ΔANE=ΔCFQ
=>NE=FQ
=>NEQF là hình bình hành
Suy ra: O là trung điểm của FE