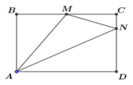
Cho hình vuông ABCD có cạnh bằng 4. Gọi M là trung điểm của CD . Tính bán kính đường trong ngoại tiếp tam giác BMD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D.
Áp dụng công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp R 2 = x 2 + r 2 với
r là bán kính đường tròn ngoại tiếp đa giác đáy
x = S O 2 - r 2 2 h : S là đỉnh hình chóp , O là tâm đường tròn ngoại tiếp đa giác đáy, h là chiều cao hình chóp
Cụ thể vào bài toán:
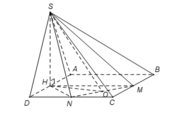
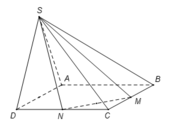
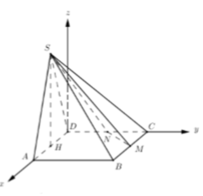
Đáy là tam giác CMN vuông tại C
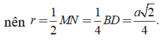
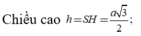
Tâm O của đường tròn ngoại tiếp tam giác CMN là trung điểm MN
Áp dụng công thức đường trung tuyến trong tam giác HMN tính được H O 2 = 5 a 2 8
Trong tam giác vuông SHO có
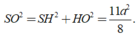
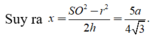
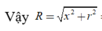
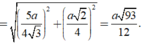

Đáp án C.
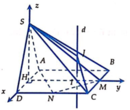
Gọi H là trung điểm của AD ![]()
Cho hệ trục tọa độ như hình vẽ => ![]()
Trung điểm MN là ![]() có
có ![]()
Gọi d là đường thẳng đi qua I và vuông góc với (ABCD)
=> d có vecto chỉ phương ![]()
∆ NCM vuông tại C => I là tâm đường tròn ngoại tiếp
=> d là trục của đường tròn ngoại tiếp tam giác CMN
=> Tâm J của mặt cầu ngoại tiếp SCMN thuộc d
Ta có d qua ![]() và
và ![]() là vecto chỉ phương
là vecto chỉ phương
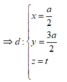
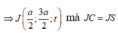
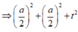
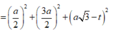
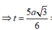 => Bán kính
=> Bán kính 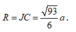




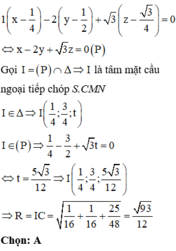

Giải bài Lê Quý Đôn trên báo KQĐ kỳ 7:
Bài 2:
Gọi I là giao điểm của AC và BD
O là tâm đường tròn ngoại tiếp \(\bigtriangleup BMD\)
H là trung điểm của MD
Ta có: ABCD là hình vuông (GT)
mà AC cắt BD tại I (GT)
\(\to \bigg\{ \begin{matrix} I&là&trung&điểm&AC \\ I&là&trung&điểm&BD \\ AC&\perp&BD&tại&I \\ \end{matrix} \)
Ta có: (O) ngoại tiếp \(\bigtriangleup BMD\) (GT)
mà I là trung điểm của BD (GT)
\(\to \begin{matrix} OI&là&đường&trung&trực&của& \bigtriangleup BMD \\ \end{matrix}\)
\(\to \begin{matrix} OI \perp BD&tại&I \\ \end{matrix} \)
mà \(\begin{matrix} AI \perp BD&tại&I&(AC \perp BD&tại&I) \\ \end{matrix}\)
\(\to OI \equiv AI\) \(\to \begin{matrix} A,&O,&I&thẳng&hàng \\ \end{matrix}\)
Xét \(\bigtriangleup ADC\), ta có: \(\bigg\{ \begin{matrix} I&là&trung&điểm&AC&(cmt) \\ M&là&trung&điểm&CD&(GT) \end{matrix}\)
\(\to \begin{matrix} IM&là&đường&trung&bình&của&\bigtriangleup ADC \\ \end{matrix}\)
\(\to IM//AD\) \(\to \begin{matrix} AIMD&là&hình&thang \end{matrix}\)
Ta có: \(\bigtriangleup OMD\) cân tại O (OM=OD do OM và OD là bán kính của (O))
mà OH là đường trung tuyến (H là trung điểm MD)
\(\to \begin{matrix} OH&là&đường&cao&của&\bigtriangleup OMD \end{matrix}\)
\(\to \begin{matrix} OH \perp MD&tại&H \\ \end{matrix}\)
mà \(\begin{matrix} AD \perp MD&tại&D&(ABCD&là&hình&vuông) \end{matrix}\)
\(\begin{matrix} AD//IM&(cmt) \end{matrix}\)
\(\to IM//OH//AD\)
Ta có: \(\bigtriangleup ABD\) vuông tại A (GT)
\(\to\) BD2= AB2 + AD2 (Định lý Pythagore)
\(\to\) BD2= 2AB2 = 2 x 42 (AB=AD do ABCD là hình vuông)
\(\to\) BD2= 32 \(\to BD = 4 \sqrt2 \)
\(\to AI=IB=\frac{BD}{2}=\frac{4\sqrt2}{2}=2\sqrt2\)
Xét hình thang AIMD, ta có: \(\bigg\{ \begin{matrix} H&trung&điểm&MD&(GT) \\ OH//&IM//&AD&(cmt) \end{matrix}\)
\(\to\) O trung điểm AI
\(\to OI=\frac{AI}{2}=\frac{2\sqrt2}{2}=\sqrt2\)
Ta có: \(\bigtriangleup OBI\) vuông tại I (\(AC\perp BD\) tại I; \(O\in AC\), \(I\in AC\); \(I\in BD\))
\(\to\) OB2= OI2 + IB2 (Định lý Pythagore) \(\to\) OB2= (\(\sqrt2 \))2 +(\(2\sqrt2\))2 = 2 + 8 = 10
\(\to OB=\sqrt{10}\)