Cho hình bình hành ABCD. Qua A kẻ đường thẳng song song với đườing chéo BD cắt các tia CB, CD tại E,F.Chứng minh rằng
a, Tứ giác ABCF là hình bình hành
b, Các đường thẳng AC,DE,BE đồng quy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 10 2017
Tứ giác ABCD là hình bình hành => AB//CD; AD//BC.
=> Giao điểm của AC; BD là trung điểm của mỗi đường
=> N là trung điểm BD (1)
Ta có: AE//BD. Mà AD//BE => Tứ giác AEBD là hình bình hành.
=> 2 đường chéo DE và AB cắt nhau tại trung điểm của mỗi đường.
=> M là trung điểm AB (2)
Tương tự: Tứ giác ABDF là hình bình hành
=> P là trung điểm AD (3)
Từ (1); (2) và (3) => G là trọng tâm của tam giác BAD.
=> AN, DM, BP đồng quy = >AC; DE; BF đồng quy (điều cần c/m).
CM
28 tháng 9 2019
a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
⇒ O là trung điểm MN
b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)
NF//AC nên B N F ^ = B A C ^ (2 góc so le trong)
Mà A C D ^ = B A C ^ (vì AB//DC, tính chất hình chữ nhật)
⇒ E M D ^ = B N F ^
Từ đó chứng minh được ∆ E D M = ∆ F B N ( g . c . g )
⇒ E M = F N
Lại có EM//FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
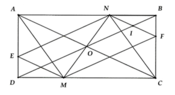
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^ v à N F B ^ = O C F ^ (đv) Þ DBFI cân tại I Þ IB = IF (1)
Ta lại chứng minh được DNIB cân tại I Þ IN = IB (2)
Từ (1) và (2) Þ I là trung điểm của NF.
12 tháng 2 2022
a: Xét tứ giác ABDF có
AB//DF
BD//AF
Do đó: ABDF là hình bình hành
Xét tứ giác ADBE có
AE/BD
BE//AD
Do đó: ADBE là hình bình hành
b: Đề sai rồi bạn