GIÚP EM BÀI 3,4 Ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


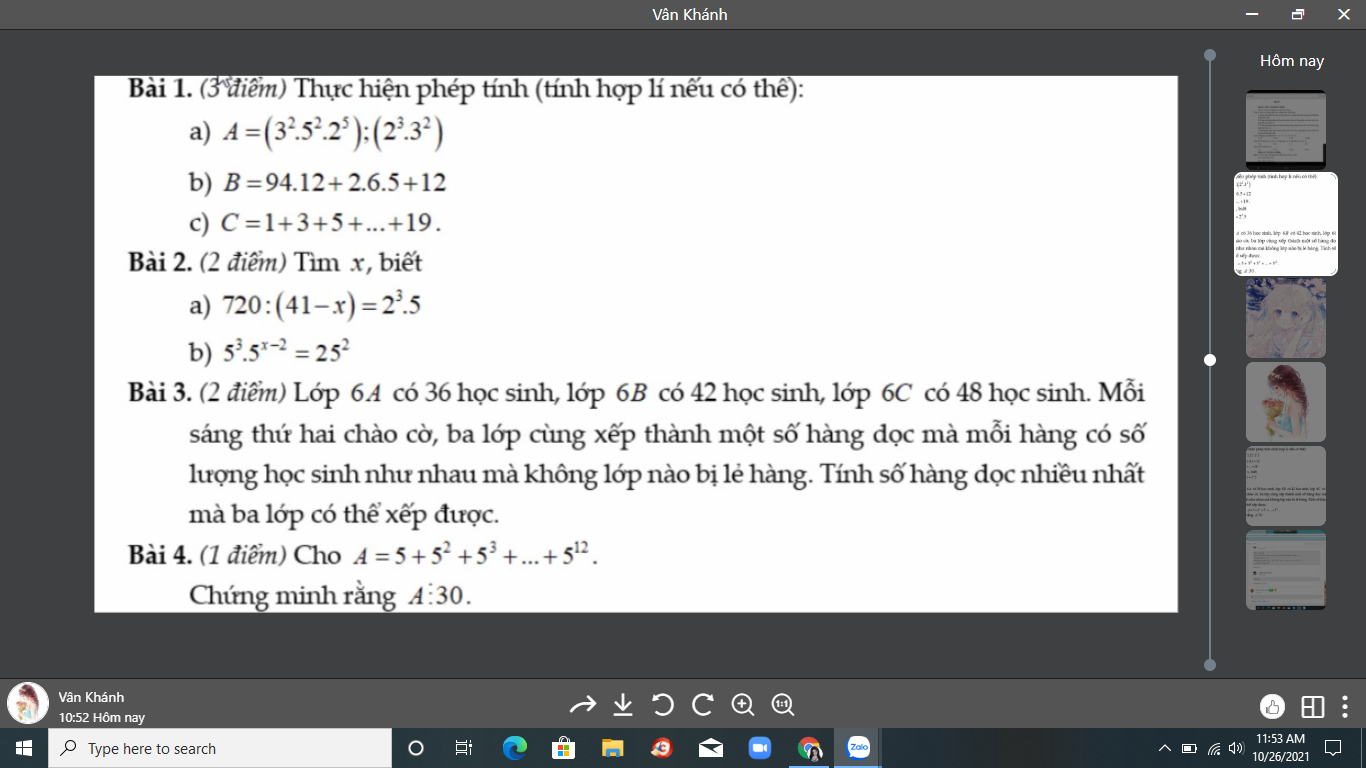
Bài 4:
\(A=5+5^2+5^3+...+5^{12}\)
\(=\left(5+5^2\right)+5^2\left(5+5^2\right)+...+5^{10}\left(5+5^2\right)\)
\(=30+5^2.30+...+5^{10}.30=30\left(1+5^2+...+5^{10}\right)⋮30\)


3:Gọi chiều dài, chiều rộng là a,b
Chu vi là 64 nên a+b=64/2=32
Theo đề, ta có hệ:
a+b=32 và (a-2)(b+3)=ab+30
=>a+b=32 và 3a-2b=36
=>a=20 và b=12

Câu 3.
\(n_{K_2O}=\dfrac{2,35}{94}=0,025mol\)
\(K_2O+H_2O\rightarrow2KOH\)
0,025 0,05 ( mol )
\(C_{M_{KOH}}=\dfrac{0,05}{0,75}=0,066M\)
Câu 4.
\(n_{Zn}=\dfrac{6,5}{65}=0,1mol\)
\(n_{HCl}=\dfrac{100.14,6\%}{36,5}=0,4mol\)
\(Zn+2HCl\rightarrow ZnCl_2+H_2\)
0,1 < 0,4 ( mol )
0,1 0,1 ( mol )
\(m_{ZnCl_2}=0,1.136=13,6g\)


1.
\(\sqrt{2x+1}=x+2\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+1\ge0\\2x+1=\left(x+2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\2x+1=x^2+4x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\x^2+2x+3=0\left(vn\right)\end{matrix}\right.\)
Phương trình đã cho vô nghiệm
2.
ĐKXĐ: \(x\ge-\dfrac{3}{2}\)
C1:
\(x^2-4x+21=6\sqrt{2x+3}\)
\(\Leftrightarrow\left(x^2-6x+9\right)+\left(2x+3-6\sqrt{2x+3}+9\right)=0\)
\(\Leftrightarrow\left(x-3\right)^2+\left(\sqrt{2x+3}-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\\sqrt{2x+3}-3=0\end{matrix}\right.\)
\(\Leftrightarrow x=3\)
C2:
\(x^2-4x+21=2.3.\sqrt{2x+3}\)
\(\Rightarrow x^2-4x+21\le3^2+2x+3\)
\(\Rightarrow x^2-6x+9\le0\)
\(\Rightarrow\left(x-3\right)^2\le0\)
\(\Rightarrow x-3=0\)
\(\Rightarrow x=3\)

Câu 4:
Số đo các góc còn lại là \(47^0;133^0;133^0\)

3: Thay y=4 vào (C), ta được:
\(5x^3-7x^2+8=12x+8\)
\(\Leftrightarrow5x^3-7x^2-12x=0\)
\(\Leftrightarrow x\left(5x^2-7x-12\right)=0\)
\(\Leftrightarrow x\left(5x-12\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{12}{5}\\x=-1\end{matrix}\right.\)

Bài 2:
Hình 3:
Xét ΔABC có AD là phân giác
nên x/3,5=7,2/4,5
=>x/3,5=1,8
=>x=6,3
Hình 4:
Xet ΔABC có MN//BC
nên 6/3=4/x
=>4/x=2
=>x=2
Bài 5
a) Ta có:
AB/A'B' = 6/4 = 3/2
AC/A'C' = 9/6 = 3/2
BC/B'C' = 12/8 = 3/2
⇒AB/A'B' = AC/A'C' = BC/B'C' = 3/2
⇒∆ABC ∽ ∆A'B'C' (c-c-c)
b) Do ∆ABC ∽ ∆A'B'C' (c-c-c)
⇒∠A = ∠A' = 100⁰
∠B = ∠B' = 44⁰
⇒∠C = 180⁰ - (∠A + ∠B)
= 180⁰ - (100⁰ + 44⁰)
= 36⁰
c) Tỉ số chu vi của ∆ABC và ∆A'B'C' là:
(AB + AC + BC)/(A'B' + A'C' + B'C')
= (6 + 9 + 12)/(4 + 6 + 8)
= 27/18
= 3/2





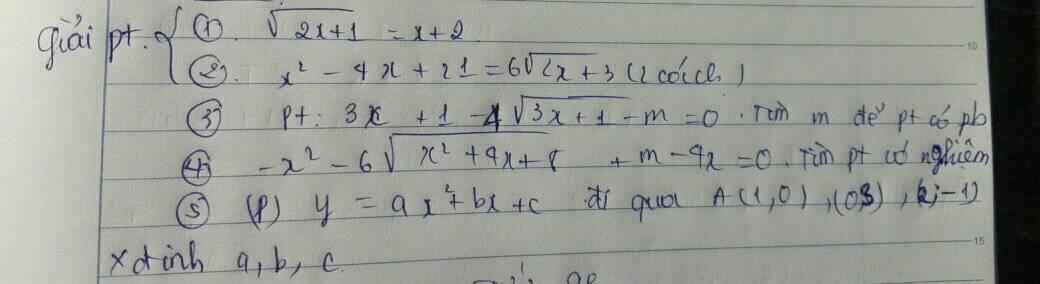 giúp em câu 3,4 với ạ
giúp em câu 3,4 với ạ


bài 3
a)trong \(\Delta ABC\) vuông tại A có
\(AB^2=BC.BH\Rightarrow BC=\dfrac{AB^2}{BH}=\dfrac{13^2}{5}=33,8\)
\(AC=\sqrt{BC^2-AB^2}\left(pytago\right)=\sqrt{33,8^2-13^2}=31,2\)
\(sinB=\dfrac{AC}{BC}=\dfrac{31,2}{33,8}=0,9\)
\(sinC=\dfrac{AB}{BC}=\dfrac{13}{33,8}=0,4\)
b)BC=BH+HC=3+4=7
trong \(\Delta ABC\) vuông tại A có
\(AC^2=BC.HC=7.4=28\Rightarrow AC=5,3\)
\(AB^2=BC.HC=7.3=21\Rightarrow AB=4,6\)
\(sinB=\dfrac{AC}{BC}=\dfrac{5,3}{7}=0,8\)
\(sinC=\dfrac{AB}{BC}=\dfrac{4,6}{7}=0,7\)
bài 4
a)A=\(cos^252^o.cos45^o+sin^252^o.cos45^o\)
A=\(cos45^o\left(cos^252^o+sin^252^o\right)\)
A=\(cos45^o=\dfrac{\sqrt{2}}{2}\)
b)\(B=tan60^o.cos^247^o+sin^247^o.tan60^o\)
B=\(tan60^o\left(cos^247^o+sin^247^o\right)\)
B=\(tan60^o=\sqrt{3}\)