Cho \(\widehat{ABC}\). Trên nửa mặt phẳng bờ ÁC không chứa điểm B, kẻ tia AN sao cho \(\widehat{NAC}=\widehat{ACB}\). Lấy điểm N trên tia đối của tia AN.
a. So sánh \(\widehat{MAB}\) và \(\widehat{ABC}\)
b. Gọi Ax là tia đối của tia AC. Tính \(\widehat{MAX}\) nếu cho \(\widehat{ACB=55^o}\)
c. Xét vị trí của tia AM đối với \(\widehat{xAB}\) trong trường hợp \(\Delta ABC\) có \(\widehat{B}=\widehat{C}\)
Giải và vẽ hình ra cho mình nhé. Mình đang cần gấp

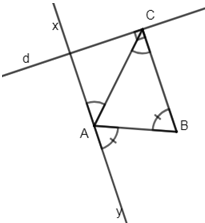
Bạn xem có phải hình vẽ thế này ko nhá!
a, \(\widehat{NAC}=\widehat{ACB}\Rightarrow\)AN//BC (2 góc so le trong bằng nhau)
\(\Rightarrow\widehat{MAB}=\widehat{ABC}\) (2 góc so le trong)
b, Do NA//BC suy ra NM//BC suy ra
\(\widehat{MAx}=\widehat{ACB}=55^o\) (2 góc đồng vị)
c, DO \(\widehat{MAx}=\widehat{ACB}\) và \(\widehat{MAB}=\widehat{ABC}\)(chứng minh trên)
Mặt khác \(\widehat{ABC}=\widehat{ACB}\left(\widehat{B}=\widehat{C}\right)\)(giả thiết)
suy ra \(\widehat{MAx}=\widehat{MAB}\)suy ra MA là tia phân giác của \(\widehat{BAx}\)