Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C y x
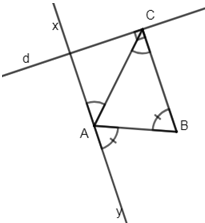
- Áp dụng tính chất tổng ba góc trong một tam giác, ta có:
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^o\) ( 1 )
- Theo đề bài ta có:
\(\widehat{BAy}=\widehat{ABC}\) , \(\widehat{xAC}=\widehat{ACB}\) ( 2 )
- Từ ( 1 ) và ( 2 ) suy ra:
\(\widehat{ABC}+\widehat{BAy}+\widehat{CAx}\) = 180o
hay Ax và Ay là 2 tia đối nhau.

A B C E F x y M I K
a) Gọi I là trung điểm của AB,
K là trung điểm của AC.
Ta có:
\(IA=IE=MK=\frac{1}{2}AB\)
\(KF=KA=IM=\frac{1}{2}AC\)
TA CÓ TAM GIÁC IAE VÀ AKF LẦN LƯỢT CÂN TẠI I VÀ K
\(\Rightarrow\widehat{EIB}=2\widehat{xAB}=42^o;\widehat{CKF}=2\widehat{CAY}=42^o\)
\(\Rightarrow\widehat{EIB}=\widehat{CKF}\)
MI//AC
=> BIM=BAC ( đồng vị) (1)
M//AB
=> MKC=BAC (đồng vị)(2)
từ (1) và (2)
\(\Rightarrow\widehat{BIM}=\widehat{MKC}\)
TỪ ĐÂY TA CÓ THỂ DỄ DÀNG CÓ EIM=MKF
=> \(\Delta EIM\)= \(\Delta MKF\)
=> ME = MF
=> TAM GIÁC MEF cân tại M

a) Ta có: ˆCAx=ˆACB(gt)���^=���^(��) mà hai góc đó là hai góc so le trong nên
suy ra Ax//BC��//�� (1)
ˆBAy=ˆABC(gt)���^=���^(��) mà hai góc đó là hai góc so le trong nên suy ra Ay//BC��//�� (2)
Từ (1) và (2) suy ra Ax và Ay cùng // BC.
Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng
bờ AB không chứa điểm C
⇒⇒ Ax và Ay là hai tia đối nhau.
b) Vì Ax và Ay là hai tia đối nhau (cmt) mà Ax//BC��//�� và Ay//BC��//��
nên suy ra xy//BC��//��
Mà BC⊥d��⊥� nên suy ra d⊥xy

Trên tia AM lấy điểm A’ sao cho AM = MA’
Dễ chứng minh được ∆AMC = ∆A’MB ( g.c.g)
A’B = AC ( = AE) và góc MAC = góc MA’B
AC // A’B => góc BAC + góc ABA’ = 180 0 (cặp góc trong cùng phía)
Mà góc DAE + góc BAC = 180 0 => góc DAE = góc ABA’
Xét ∆DAE và ∆ABA’ có : AE = A’B , AD = AB (gt)
góc DAE = góc ABA’ ∆DAE = ∆ABA’(c.g.c)
góc ADE = góc BAA’ mà góc HAD + góc BAA’ = 90 0
=> góc MAD + góc ADE = 90 0 . Suy ra MA vuông góc với DE

A M B C N D x y
a) Vì \(\widehat{AMx}=\widehat{B}\), hai góc này ở vị trí đồng vị nên Mx // BC.
Giả sử Mx không cắt AC. Suy ra Mx // AC. Mx // AC, Mx // BC nên AC // BC(mâu thuẫn với giả thiết ABC là tam giác). Vậy Mx cắt AC
b) Vì \(\widehat{CNy}=\widehat{C}\), hai góc này ở vị trí so le trong nên Ny // BC.
Ny // BC, Mx // BC nên Mx // Ny.