Cho parabol (p): ax2+bx+1
Biết rằng 33 parabol đó đi qua 2 điểm A(1;4) và B(-1;2) parabol đó là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PN
Phạm Ngọc
26 tháng 10 2018
https://i.imgur.com/nsNtpfc.jpg
Đúng(0)
Những câu hỏi liên quan
CM
28 tháng 6 2017
+ Parabol y = ax2 + bx + 2 đi qua M(1 ; 5)
⇒ 5 = a.12 + b.1 + 2 ⇒ a + b = 3 (1) .
+ Parabol y = ax2 + bx + 2 đi qua N(–2; 8)
⇒ 8 = a.( –2)2 + b.( –2) + 2 ⇒ 4a – 2b = 6 (2).
Từ (1) và (2) suy ra: a = 2; b = 1.
Vậy parabol cần tìm là y = 2x2 + x + 2.
CM
11 tháng 5 2018
+ Parabol y = ax2 + bx + 2 đi qua điểm B(–1 ; 6)
⇒ 6 = a.( –1)2 + b.( –1) + 2 ⇒ a = b + 4 (1)
+ Parabol y = ax2 + bx + 2 có tung độ của đỉnh là –1/4
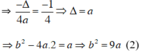
Thay (1) vào (2) ta được: b2 = 9.(b + 4) ⇔ b2 – 9b – 36 = 0.
Phương trình có hai nghiệm b = 12 hoặc b = –3.
Với b = 12 thì a = 16.
Với b = –3 thì a = 1.
Vậy có hai parabol thỏa mãn là y = 16x2 + 12b + 2 và y = x2 – 3x + 2.
CM
3 tháng 4 2018
Vì parabol đi qua ba điểm A, B, C nên ta có hệ phương trình:
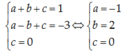
Vậy (P): y = -x2 + 2x
Chọn C.
CM
14 tháng 5 2017
+ Parabol y = ax2 + bx + 2 có trục đối xứng x = –3/2
⇒ –b/2a = –3/2 ⇒ b = 3a (1)
+ Parabol y = ax2 + bx + 2 đi qua điểm A(3; –4)
⇒ –4 = a.32 + b.3 + 2 ⇒ 9a + 3b = –6 (2).
Thay b = 3a ở (1) vào biểu thức (2) ta được:
9a + 3.3a = –6 ⇒ 18a = –6 ⇒ a = –1/3 ⇒ b = –1.
Vậy parabol cần tìm là y = –1/3x2 – x + 2.
14 tháng 11 2022
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b+c=-1\\\dfrac{-b}{2a}=-2\\-\dfrac{b^2-4ac}{4a}=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=4a\\a+b+c=-1\\b^2-4ac=-20a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4a\\c=-1-a-b=-1-a-4a=-1-5a\\16a^2-4a\left(-5a-1\right)=-20a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}16a^2+20a^2+4a+20a=0\\b=4a\\c=-5a-1\end{matrix}\right.\)
=>a=-2/3; b=-8/3; c=10/3-1=7/3
23 tháng 10 2020
parabol y= ax2+bx+c đi qua A(2,-7)
\(\Rightarrow-7=a.2^2+b.2+c\)
\(\Rightarrow-7=4a+2b+c\)
\(\Rightarrow4a+2b+c=-7\)(1)
parabol y=ax2+bx+c đi qua B (-5,0)
\(\Rightarrow0=a\left(-5\right)^2+b.\left(-5\right)+c\)
\(\Rightarrow0=25a-5b+c\)
\(\Rightarrow25a-5b+c=0\)(2)
parabol có trục đối cứng là x=2 nên ta có
\(\frac{-b}{2a}=2\Leftrightarrow-b=4a\Leftrightarrow4a+b=0\left(3\right)\)
từ (1) ,(2) và (3) ta có hệ phương trình
\(\left\{{}\begin{matrix}4a+2b+c=-7\\25a-5b+c=0\\4a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\frac{1}{7}\\b=\frac{-4}{7}\\c=\frac{-45}{7}\end{matrix}\right.\)
đây là theo cách mình làm thôi k hắc là đúng hya sai đâu cho dù sai bạn cũng dựa vào cái kiểu này mà tính nhé
CM
14 tháng 1 2017
(P): y = ax2 + bx + c
Parabol đi qua A(0 ; –1) ⇒ –1 = a.02 + b.0 + c ⇒ c = –1.
Parabol đi qua B(1 ; –1) ⇒ –1 = a.12 + b.1 + c ⇒ a + b + c = –1.
Mà c = –1 ⇒ a + b = 0 (1)
Parabol đi qua C(–1; 1) ⇒ a.(–1)2 + b.(–1) + c = 1 ⇒ a – b + c = 1.
Mà c = –1 ⇒ a – b = 2 (2)
Từ (1) và (2) ⇒ a = 1; b = –1.
Vậy a = 1 ; b = –1 ; c = –1.
CM
6 tháng 6 2019
(P) : y = ax2 + bx + c
Parabol có đỉnh I(1 ; 4) ⇒ –b/2a = 1 ⇒ b = –2a ⇒ 2a + b = 0.
Parabol đi qua I(1; 4) ⇒ 4 = a.12 + b . 1 + c ⇒ a + b + c = 4.
Paraol đi qua D(3; 0) ⇒ 0 = a.32 + b.3 + c ⇒ 9a + 3b + c = 0.
Giải hệ phương trình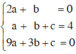 
ta được : a = –1 ; b = 2 ; c = 3.
Vậy a = –1 ; b = 2 ; c = 3.