Cho y= (2m+1)x+n (2)
a) Tìm m và n để đường thẳng (2) cắt trục tung tại điểm y=\(1-2\sqrt{2}\)và cắt trục hoành tại điểm x=1
b) Tìm m và n để đường thẳng (2) cắt đường thẳng y=\(\frac{1}{2}x+1\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích các bước giải:
a/ Thế x=-1 và y=2 vào (d) ta được:
2=(m-2).(-1)+n
⇔ -(m-2)+n=2
⇔ -m+2+n=2
⇔ -m+n=0
⇔ n-m=0 (1)
Thế x=3 và y=-4 vào (d) ta được:
-4=(m-2).3+n
⇔ 3m-6+n=-4
⇔ n+3m=2 (2)
Từ (1) và (2) ta có hệ phương trình:
{n−m=0n+3m=2{n−m=0n+3m=2
⇔ {n=mm+3m=2{n=mm+3m=2
⇔ {n=m4m=2{n=m4m=2
⇔ {n=mm=1/2(nhận){n=mm=1/2(nhận)
⇔ {n=m=1/2m=1/2{n=m=1/2m=1/2
Vậy m=n=1/2.
b/ (d) cắt trục tung tại điểm có tung độ bằng 1-√2
⇒ x=0 ; y=1-√2 (1)
(d) cắt trục hoành tại điểm có hoành độ bằng 2+√2
⇒ x=2+√2 ; y=0 (2)
Thế (1) vào (d) ta được:
1-√2=(m-2).0+n
⇔ n=1-√2
Thế (2) ; n=1-√2 vào (d) ta được:
0=(m-2).(2+√2)+(1-√2)
⇔ 2m+√2m-4+√2+1-√2=0
⇔ 2m+√2m-3=0
⇔ (2+√2)m=3
⇔ m=6-3√2/2 (nhận)
Vậy n=1-√2 ; m=6-3√2/2.

Đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1 - 2 2 nên ta có n = 1 - 2
Đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 2 + 2 nên ta có:
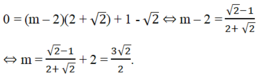
Trả lời: Khi n = 1 -
2
và 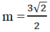 thì đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1 -
2
và cắt trục hoành tại điểm có hoành độ 2 +
2
thì đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1 -
2
và cắt trục hoành tại điểm có hoành độ 2 +
2

a: Thay x=-1 và y=2 vào (d), ta được:
\(-\left(m-2\right)+n=2\)
=>-m+2+n=2
=>-m+n=0
=>m-n=0(1)
Thay x=3 và y=-4 vào (d), ta được:
\(3\left(m-2\right)+n=-4\)
=>3m-6+n=-4
=>3m+n=2(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}m-n=0\\3m+n=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m-n+3m+n=2\\m-n=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m=2\\n=m\end{matrix}\right.\Leftrightarrow n=m=\dfrac{1}{2}\)
b: Thay x=0 và \(y=1-\sqrt{2}\) vào (d), ta được:
\(0\left(m-2\right)+n=1-\sqrt{2}\)
=>\(n=1-\sqrt{2}\)
Vậy: (d): \(y=\left(m-2\right)x+1-\sqrt{2}\)
Thay \(x=2+\sqrt{2}\) và y=0 vào (d), ta được:
\(\left(m-2\right)\cdot\left(2+\sqrt{2}\right)+1-\sqrt{2}=0\)
=>\(\left(m-2\right)\left(2+\sqrt{2}\right)=\sqrt{2}-1\)
=>\(m-2=\dfrac{\sqrt{2}-1}{2+\sqrt{2}}=\dfrac{-4+3\sqrt{2}}{2}\)
=>\(m=\dfrac{-4+3\sqrt{2}+4}{2}=\dfrac{3\sqrt{2}}{2}\)
c: 2y+x-3=0
=>2y=-x+3
=>\(y=-\dfrac{1}{2}x+\dfrac{3}{2}\)
Để (d) vuông góc với đường thẳng y=-1/2x+3/2 thì
\(-\dfrac{1}{2}\left(m-2\right)=-1\)
=>m-2=2
=>m=4
Vậy: (d): \(y=\left(4-2\right)x+n=2x+n\)
Thay x=1 và y=3 vào y=2x+n, ta được:
\(n+2\cdot1=3\)
=>n+2=3
=>n=1
d: 3x+2y=1
=>\(2y=-3x+1\)
=>\(y=-\dfrac{3}{2}x+\dfrac{1}{2}\)
Để (d) song song với đường thẳng \(y=-\dfrac{3}{2}x+\dfrac{1}{2}\) thì
\(\left\{{}\begin{matrix}m-2=-\dfrac{3}{2}\\n\ne\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=\dfrac{1}{2}\\n\ne\dfrac{1}{2}\end{matrix}\right.\)
Vậy: (d): \(y=\left(\dfrac{1}{2}-2\right)x+n=-\dfrac{3}{2}x+n\)
Thay x=1 và y=2 vào (d), ta được:
\(n-\dfrac{3}{2}=2\)
=>\(n=2+\dfrac{3}{2}=\dfrac{7}{2}\left(nhận\right)\)

1) Hai đường thẳng cắt nhau tại một điểm trên trục tung khi \(\int^{a\ne a^,}_{b=b^,}\Rightarrow\int^{2\ne3}_{5m-4=-2m+1}\)
=> 7m=5 => m= 5/7
2) y=5x+1-2m : Với y=0 =>5x +1-2m =0 => x =(2m-1)/5
y =x - m -4 : Với y =0 => x= m + 4
Để hai đường thẳng cắt nhau tại một điểm trên trục hoành thì:\(\int^{1\ne5}_{\frac{2m-1}{5}=m+4}\)
=> 2m-1=5m+20 => m=-7