Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 2:
a: Xet ΔABC có AD/AB=AF/AC
nen DF//BC và DF=1/2BC
=>BDFC là hình thang
mà góc B=góc C
nên BDFC là hình thang cân
b Xet ΔABC có
CE/CB=CF/CA
nên EF//AB và EF=AB/2
=>EF//AD và EF=AD
=>ADEF là hình bình hành
mà AD=AF
nen ADEF là hình thoi
c: Để ADEF là hình vuông thì góc BAC=90 độ
a) Xét tứ giác ADEF có : góc A = 90 độ ( tam giác ABC vuông tại A)
góc EFA = 90 độ ( EF vuông góc với AB tại F)
góc EDA = 90 ( ED vuông góc với AC tại D)
suy ra : ADEF là hcn
b) Xét tam giác ABC có : BE = EC ( E là trung điểm của BC )
ED song song với AB ( EFAD là hcn )
suy ra : AD = DC
Xét tứ giác AECK có : ED = DK ( E đối xứng với K qua D )
AD = DC (cmt)
suy ra : tứ giác AECK là hình bình hành
mà ED vuông góc với AC
suy ra : hbh AECK là hình thoi
a: Xét ΔABC có
BE/BC=BD/BA
nên ED//AC và ED=AC/2
=>ED//AF và ED=AF
=>ADEF là hình bình hành
mà góc FAD=90 độ
nên ADEF là hình chữ nhật
b: Xét tứ giác BMAE có
D là trung điểm chung của BA vàME
EA=EB
Do đó: BMAE là hình thoi
c: \(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
S=1/2*3*4=6(cm2)
https://lazi.vn/edu/exercise/cho-tam-giac-abc-goi-d-e-f-theo-thu-tu-la-trung-diem-cua-ab-bc-ca-goi-m-n-p-q-theo-thu-tu-la-trung-diem
Bạn xem tại link này nhé
Học tốt!!!!!!
a: Xét tứ giác ADEF có
\(\widehat{ADE}=\widehat{AFE}=\widehat{DAF}=90^0\)
=>ADEF là hình chữ nhật
b: Xét ΔABC có
E là trung điểm của CB
ED//AB
Do đó: D là trung điểm của AC
Xét tứ giác AECK có
D là trung điểm chung của AC và EK
=>AECK là hình bình hành
Hình bình hành AECK có AC\(\perp\)EK
nên AECK là hình thoi
c: Xét ΔABC có
E,D lần lượt là trung điểm của CB,CA
=>ED là đường trung bình của ΔABC
=>\(ED=\dfrac{AB}{2}\)
mà \(ED=\dfrac{EK}{2}\)
nên EK=AB
Ta có: ED//AB
D\(\in\)EK
Do đó: EK//AB
Ta có: ADEF là hình chữ nhật
=>AE cắt DF tại trung điểm của mỗi đường
=>O là trung điểm chung của AE và DF
Xét tứ giác ABEK có
KE//AB
KE=AB
Do đó: ABEK là hình bình hành
=>AE cắt BK tại trung điểm của mỗi đường và AE=BK
mà O là trung điểm của AE
nên O là trung điểm của BK
=>B,O,K thẳng hàng
ΔEMA vuông tại M
mà MO là đường trung tuyến
nên \(MO=\dfrac{AE}{2}\)
mà AE=DF
nên \(MO=\dfrac{DF}{2}\)
Xét ΔDMF có
MO là đường trung tuyến
MO=DF/2
Do đó: ΔDMF vuông tại M
=>\(\widehat{DMF}=90^0\)
Ta có: E là trung điểm của BC (gt)
D là trung điểm của AB (gt) nên ED là đường trung bình của ∆ ABC
DE = AF = 1/2 AC (1)
F là trung điểm của AC (gt) nên EF là đường trung bình ∆ ABC ⇒ EF = AD = 1/2 AB (2)
AB = AC (gt)
Từ (1), (2) và (gt) suy ra: AD = DE = EF = AF
Vậy tứ giác ADEF là hình thoi.
a: Xét ΔABC có AD/AB=AE/AC
nên DE//BC và DE=BC/2
=>DE//BF và DE=BF
=>BDEF là hình bình hành
b: Xét ΔBAC có BD/BA=BF/BC
nên DF//AC và DF=AC/2
=>DF=EK
Xét tứ giác DEFK cos
DE//FK
DF=EK
Do đó: DEFK là hình thang cân
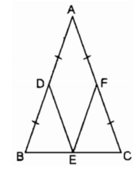
a: Xét ΔABCcó CE/CB=CF/CA
nên EF//AB và EF=AB/2
=>EF//AD và EF=AD
=>ADEF là hình bình hành
mà AD=AF
nên ADEF là hình thoi
b: Xét tứ giác AECM có
F là trung điểm chung của AC và EM
nên AECM là hình bình hành
mà góc AEC=90 độ
nên AECM là hình chữ nhật
c: Xét tứ giác AMEB có
AM//BE
AM=BE
Do đó: AMEB là hình bình hành
Suy ra: AE cắt MB tại trung điểm của mỗi đường(1)
Vì ADEF là hình thoi
nên AE cắt DF tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AE,DF,BM đồng quy
d: Để ADEF là hình vuông thì góc BAC=90 độ