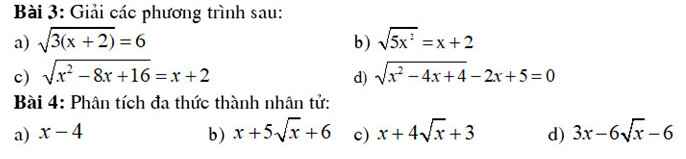giải giúp mình bài 3,4 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
B
Buddy
19 tháng 9 2021
Đúng(0)
Những câu hỏi liên quan
DN
4
11 tháng 7 2017
3,4 - x + 1,7 = 1,05
x + 1,7 = 3,4 - 1,05
x + 1,7 = 2,35
x = 2,35 - 1,7
x = 0,65
PV
2
14 tháng 6 2023
4:
a: A=1/3(1+1/2+...+1/64)
Đặt B=1+1/2+...+1/64
=>2B=2+1+...+1/32
=>B=2-1/64=127/64
=>A=1/3*127/64=127/192
b: =5/2(1-1/3+1/3-1/5+...+1/11-1/13)
=5/2*12/13
=60/26=30/13
30 tháng 8 2021
Bài 4:
a: \(x-4=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)
b: \(x+5\sqrt{x}+6=\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)\)
c: \(x+4\sqrt{x}+3=\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)\)
d: \(3x-6\sqrt{x}-6=3\left(x-\sqrt{x}-2\right)=3\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
30 tháng 8 2021
Bài 3:
a) \(\sqrt{3\left(x+2\right)}=6\left(đk:x\ge-2\right)\)
\(\Leftrightarrow3\left(x+2\right)=36\)
\(\Leftrightarrow3x=30\Leftrightarrow x=10\)(thỏa đk)
b) \(\sqrt{5x^2}=x+2\left(đk:x\ge-2\right)\)
\(\Leftrightarrow5x^2=\left(x+2\right)^2\)
\(\Leftrightarrow4x^2-4x-4=0\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=\dfrac{5}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=\dfrac{\sqrt{5}}{2}\\x-\dfrac{1}{2}=-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1+\sqrt{5}}{2}\\x=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)(thỏa đk)
c) \(\sqrt{x^2-8x+16}=x+2\left(1\right)\left(đk:x\ge-2\right)\)
\(\Leftrightarrow\sqrt{\left(x-4\right)^2}=x+2\Leftrightarrow\left|x-4\right|=x+2\)
TH1: \(x\ge4\)
\(\left(1\right)\Leftrightarrow x-4=x+2\Leftrightarrow-4=2\)(vô lý)
TH2: \(-2\le x< 4\)
\(\left(1\right)\Leftrightarrow4-x=x+2\)
\(\Leftrightarrow x=1\)(thỏa đk)
d) \(\sqrt{x^2-4x+4}-2x+5=0\left(đk:x\ge\dfrac{5}{2}\right)\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}-2x+5=0\left(2\right)\Leftrightarrow\left|x-2\right|-2x+5=0\)
TH1: \(x\ge2\)
\(\left(2\right)\Leftrightarrow x-2-2x+5=0\)
\(\Leftrightarrow x=3\)(thỏa đk)
TH2: \(\dfrac{5}{2}\le x< 2\)
\(\left(2\right)\Leftrightarrow2-x-2x+5=0\)
\(\Leftrightarrow x=\dfrac{7}{3}\)(không thỏa đk)
Bài 4:
a) \(x-4=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)
b) \(x+5\sqrt{x}+6=\left(\sqrt{x}+\dfrac{5}{2}\right)^2-\dfrac{1}{4}=\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)\)
c) \(x+4\sqrt{x}+3=\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)\)
d) \(3x-6\sqrt{x}-6=3\left(\sqrt{x}-1-\sqrt{3}\right)\left(\sqrt{x}-1+\sqrt{3}\right)\)
AH
Akai Haruma
Giáo viên
6 tháng 1
Bài 4:
Quãng đường bạn An đi: $BD$
Quãng đường bạn Hải đi: $CD$
Do $AB\parallel NC$ nên áp dụng định lý Talet, tỉ số quãng đường bạn An đi so với bạn Hải đi là:
$\frac{BD}{CD}=\frac{AB}{NC}=\frac{AB}{AM}=\frac{1}{2}$
Vậy bạn An đi quãng đường bằng 1/2 quãng đường Hải đi
Mà vận tốc 2 bạn như nhau nên thời gian An đi bằng 1/2 thời gian Hải đi
Bạn An đến D lúc 8h, xuất phát từ 7h30 nên thời gian An đi là: 8h-7h30'=30'=0,5h
Thời gian Hải đi để đến gặp An lúc 8h là: $0,5.2=1$ (h)
Vậy Hải phải xuất phát lúc: $8h-1h=7h$
AH
Akai Haruma
Giáo viên
6 tháng 1
Bài 3:
a. Xét tam giác $ADC$ có $MP\parallel DC$ nên áp dụng định lý Talet:
$\frac{AM}{MD}=\frac{AP}{PC}(1)$
Xét tam giác $ACB$ có $PN\parallel AB$ nên áp dụng định lý Talet:
$\frac{AP}{PC}=\frac{BN}{NC}(2)$
Từ $(1); (2)\Rightarrow \frac{AM}{MD}=\frac{BN}{NC}$
b.
Áp dụng định lý Talet với tam giác $ADC$, $MP\parallel DC$:
$\frac{MP}{DC}=\frac{AM}{AD}=\frac{AM}{AM+MD}=\frac{AM}{AM+2AM}=\frac{1}{3}$
$\Rightarrow MP=DC:3=6:3=2$ (cm)
Theo kết quả phần a:
$\frac{BN}{NC}=\frac{AM}{MD}=\frac{AM}{2AM}=\frac{1}{2}$
$\Rightarrow NC=2BN$
Áp dụng định lý Talet cho tam giác $ACB$, có $PN\parallel AB$:
$\frac{PN}{AB}=\frac{CN}{CB}=\frac{CN}{CN+BN}=\frac{2BN}{2BN+BN}=\frac{2}{3}$
$\Rightarrow PN=\frac{2}{3}AB=\frac{2}{3}.4=\frac{8}{3}$ (cm)
$MN=MP+PN=2+\frac{8}{3}=\frac{14}{3}$ (cm)
1 tháng 7 2023
3:Gọi chiều dài, chiều rộng là a,b
Chu vi là 64 nên a+b=64/2=32
Theo đề, ta có hệ:
a+b=32 và (a-2)(b+3)=ab+30
=>a+b=32 và 3a-2b=36
=>a=20 và b=12
11 tháng 7 2017
1,2 + 2,3 + 3,4 - 4,5 + 5,6 - 6,7 + 7,8 - 8,9 + 9,1 = 9,3
ZT
15 tháng 3 2022
Ôn tập để thi tốt thì bạn nên tự làm nhé
Chứ bạn hỏi thì bài ôn ra chẳng để lm j