cho nửa đường tròn (O) , đường kinh AB. trên AB lấy các điểm M,N sao cho AM=BN. Qua M,N kẻ đường song sing với nhau cắt nuwae đg tròn llần lượt tại C,D chứng CD và ND vuông góc CD
giúp mình với cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 6 2018
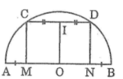
Ta có: MC // ND (gt)
Suy ra tứ giác MCDN là hình thang
Lại có: OM + AM = ON + BN (= R)
Mà AM = BN (gt)
Suy ra: OM = ON
Kẻ OI ⊥ CD (3)
Suy ra: IC = ID (đường kính dây cung)
Khi đó OI là đường trung bình của hình thang ACDN
Suy ra: OI // MC // ND (4)
Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.
AH
Akai Haruma
Giáo viên
17 tháng 9 2021
Lời giải:
Kẻ đường kính $CT$ của $(O)$ thì $O$ là trung điểm $CT$
Xét tứ giác $CNTM$ có 2 đường chéo $CT,MN$ cắt nhau tại trung điểm $O$ của mỗi đường nên $CNTM$ là hình bình hành.
$\Rightarrow CM\parallel NT$. Mà CM\parallel DN$ nên $DN\parallel NT$ hay $D,N,T$ thẳng hàng.
Ta có: $\widehat{CDN}=\widehat{CDT}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow CD\perp DN$. Mà $DN\parallel MC$ nên $CD\perp MC$ (đpcm)
