K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
12 tháng 6 2018
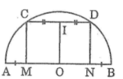
Ta có: MC // ND (gt)
Suy ra tứ giác MCDN là hình thang
Lại có: OM + AM = ON + BN (= R)
Mà AM = BN (gt)
Suy ra: OM = ON
Kẻ OI ⊥ CD (3)
Suy ra: IC = ID (đường kính dây cung)
Khi đó OI là đường trung bình của hình thang ACDN
Suy ra: OI // MC // ND (4)
Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.

Lời giải:
Kẻ đường kính $CT$ của $(O)$ thì $O$ là trung điểm $CT$
Xét tứ giác $CNTM$ có 2 đường chéo $CT,MN$ cắt nhau tại trung điểm $O$ của mỗi đường nên $CNTM$ là hình bình hành.
$\Rightarrow CM\parallel NT$. Mà CM\parallel DN$ nên $DN\parallel NT$ hay $D,N,T$ thẳng hàng.
Ta có: $\widehat{CDN}=\widehat{CDT}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow CD\perp DN$. Mà $DN\parallel MC$ nên $CD\perp MC$ (đpcm)
Hình vẽ:
